Внешняя алгебра, которую мы заслужили. Часть 2 — полиформы и графы

В данной работе мы продолжаем обзор свойств внешней алгебры. В первой части мы определили внешнее произведение элементов, ввели понятие симплексов, границ и копространства. Здесь рассмотрим аффинные пространства, в которых определено скалярное произведение между элементами, их называют также евклидовыми.

Обычно в качестве примера евклидового приводят окружающее нас трехмерное пространство. В нем действительно есть скалярное произведение между элементами и векторами. Но все-таки оно является лишь частным случаем общего семейства евклидовых пространств. Более общим примером являются пространства со связями, в простонародье именуемые графами. Поэтому в основном на метрических свойствах графах мы и сосредоточимся. Покажем, как построить полиформу для заданного графа, и на ее основе определять его метрические свойства. Например, остовное число или резистивную дистанцию. Последняя в электрических сетях совпадает с эффективным сопротивлением между узлами.

Полиформа графа строится на основании его связей. Но можно идти и обратным путем - от расстояний между элементами. Так строится дуальная полиформа и она более подходит для описания обычного (геометрического) пространства.

Также кратко коснемся представления в виде полиформ и направленных графов (орграфов). В направленном графе у вершин появляются разные потенциалы. Которые, например, можно использовать для их ранжирования (да, это про PageRank).

Билинейная и квадратичная формы

Поскольку в евклидовом пространстве есть дополнительное (по отношению к просто аффинному) свойство, то нам надо определить сущность, которая это свойство выражает. Принято, что таким свойством является билинейная форма. Что это за зверь такой? Проще всего пока считать билинейную форму еще одним типом произведения. Аргументами формы (множителями произведения) могут быть произвольные цепи (либо коцепи) с обязательным условием, что порядок у обоих аргументов одинаков (напомним, что цепи - это линейные комбинации симплексов). Но чаще всего аргументами форм будут границы (поливекторы). Вот пример формы двух векторов (ab) и (bc) :

$F(ab, bc) == \langle ab, bc\rangle$

Данное выражение просто показывает, что форму мы будем обозначать угловыми скобками. Можно было бы и каким-нибудь знаком умножения между векторами обозначить форму, но непонятно, какой символ использовать, да и угловые скобки для обозначения форм в принципе общеприняты. Еще один момент - внутри формы мы опустили круглые скобки для обозначения границ (векторов). То есть ab==(ab) . Связано это с тем, что далее мы будем иметь дело большей частью с границами и не хотим отягощать выражения большим количеством скобок.

Если форма - это произведение, то чему равен его результат? Это хороший вопрос, ответ на который простой - ничему. Форма - это и есть результат произведения. То есть форма просто связывает (объединяет) свои аргументы. Этим форма похожа на внешнее произведение. Но в отличие от него, аргументами формы может быть один и тот же элемент. Такие формы называют квадратичными (иногда - квадратными). Чтобы не повторять дважды один и тот же аргумент, будем обозначать квадратичные формы степенью:

$\langle ab, ab \rangle == \langle ab \rangle^2$

Здесь степень - это просто напоминание, что форма квадратичная.

Почему форма - билинейная? Потому что подчиняется закону дистрибутивности, как и любое произведение, то есть линейна по аргументам. Если какой-либо аргумент формы является суммой, то форму можно представить в виде суммы форм. Также можно выносить из аргументов скалярный множитель (или знак):

$\langle ab+bc, ab \rangle = \langle ab \rangle^2 + \langle bc, ab \rangle, \quad \langle ab, -2bc \rangle = -2\langle ab, bc \rangle$

Теперь внимание. Формы можно умножать и складывать между собой. Сложение мы уже видели, а что с умножением? При умножении двух форм перемножаются их аргументы - левый с левым, правый с правым. Пожалуй, это основное свойство форм, которое мы тут вводим. Умножение аргументов - это их внешнее произведение. То, которое мы рассматривали в предыдущей части. Поэтому если перемножаемые границы (аргументы) имеют общую вершину, то они сливаются в одну:

$\langle ab, ac \rangle*\langle bc \rangle^2 = \langle ab*bc, ac*bc \rangle = \langle abc \rangle^2$

Порядок результата произведения, равен сумме порядков перемножаемых форм (порядок формы - это порядок ее аргументов).

Также как существует единичный симплекс, существует и тождественная (единичная) форма, при умножении на которую произвольная форма не меняется: $E*\langle ab, bc \rangle = \langle ab, bc \rangle$ .

Для начала достаточно. Едем дальше.

Полиформы

На конечном множестве вершин можно определить предельную границуи соответствующую ей предельную форму $\langle I \rangle^2$ . Предельная форма на 4-х вершинах a, b, c, d имеет 3-й порядок и равна $\langle abcd \rangle^2$ . Единичная формаимеет 0-й порядок - это скалярная форма. Векторная форма $\langle ab \rangle^2$ имеет 1-й порядок и т.д. В промежутке от нулевого до предельного порядка существуют разнообразные формы промежуточных порядков. Из них можно образовать линейную комбинацию, - то есть присвоить каждой форме некий коэффициент и сложить. Подобные комбинации форм будем называть полиформами. Пример полиформы на трех вершинах:

$W(a, b, c) = E + \langle ab\rangle^2 + 2\langle ab, ac \rangle + 3\langle abc \rangle^2$

Каждое слагаемое данной полиформы называется формой-мономом. Полная полиформа всегда содержит предельную форму для заданного множества вершин. Произведение любой формы-монома полиформы на ее предельную форму дает ноль.

Слагаемые полиформы могут быть объединены по величине порядка форм-мономов. Каждая такая сумма имеет свой порядок (грейд), поэтому удобно такие называть грейд-формами.

Поскольку количество новых терминов растет (а мы только начали), то пора уже заземлиться и привязаться к какому-либо известному понятию. У нас уже достаточно определений, чтобы ввести полиформу связи. Вот она - связь элементов:

а вот ее полиформа: $W(a, b) = E + p_{ab} \langle ab\rangle^2$ .

Здесь $p_{ab}$ - величина связи. В простых графах связи принимают равными единице.

Почему полиформа связи имеет именно такой вид? Никто не знает (шутка). Можно сказать, что это установлено опытным путем. Полиформу связи будем называть также фактор-формой, - далее станет понятно почему.

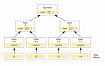
Можете догадаться, какой вид имеет полиформа двух связей? Ну да, стоит уточнить - двух связанных связей, то есть на трех вершинах. Пусть для простоты величина связей равна 1 (мы можем ввести коэффициенты позже), тогда последовательное связывание трех вершин образует граф-путь (маршрут) a - b- c . Полиформа маршрута будет равна произведению полиформ каждой его связи - вот так вот просто:

$Path(abc) = (E + \langle ab\rangle^2)*(E + \langle bc\rangle^2)$

Это факторное представление полиформы графа, то есть произведение фактор-форм его связей. Можно раскрыть скобки и используя правила произведения форм получить линейное разложение полиформы:

$Path(abc) = E + \langle ab\rangle^2 + \langle bc\rangle^2 + \langle abc\rangle^2$

Общий метод получения полиформы графа теперь понятен, да? Полиформа графа - это произведение фактор-форм его связей.

Для получения полиформы цикла на трех вершинах нам надо добавить в маршрут еще одну связь. Получим:

$Cycle(abc) = (E + \langle ab\rangle^2)*(E + \langle bc\rangle^2)*(E + \langle ca\rangle^2) = E + \langle ab\rangle^2 + \langle bc\rangle^2 + \langle ca\rangle^2 + 3\langle abc\rangle^2$

Источник: https://habr.com/ru/post/544732/

Вернуться к списку

Интересные статьи

Курс по C++ в CS центре, вторая часть

Computer Science Center — это совместная инициатива Computer Science клуба при ПОМИ РАН, компании JetBrains и Школы анализа данных Яндекса. Центр существует, чтобы дать возможность талантливым...

SamsPcbGuide, часть 11: Технологии, корпуса BGA-типа и космос

В обсуждениях к предыдущей статье proton17 написал, что в космос обычные BGA не летают, дав ссылки на корпуса CCGA-типа как образец надёжности. Я решил разобраться в этом вопросе и нашёл много ин...

Maltego ближе к телу. Часть 2

Здравствуйте, дорогие друзья. Вот, наконец-то, и добрался я до написания второй статьи, посвященной Maltego. Кто не читал первую – обязательно прочитайте вот тут. В ней я писал, что же такое Malt...

Резервное копирование, часть 4: Обзор и тестирование zbackup, restic, borgbackup

В данной статье будут рассматриваться программные средства для резервного копирования, которые путем разбиения потока данных на отдельные компоненты (chunks), формируют репозиторий. Компоненты...

Назад к микросервисам вместе с Istio. Часть 3

Прим. перев.: Первая часть этого цикла была посвящена знакомству с возможностями Istio и их демонстрации в действии, вторая — тонко настраиваемой маршрутизации и управлению сетевым трафиком. ...