Язык — это механизм, который позволяет конструировать все возрастающую сложность из отдельно взятых преобразований. Статья является продолжением идей, которые в свое время высказали кибернетики В. Турчин и Р. Эшби.
Сначала о более фундаментальном. О вещи или явлении как об ограничении разнообразия [1, c 187]

Это ограничение (рис. - консольный вывод программы) таково, что при переходах состояний с учетом операторов оно явно больше, чем без них. В примере: множество состояний {22, 12, 21, 11}, множество операторов {55, 54, 45, 44}. Из состояния 22 следуют состояния 12, 22, 11, 21. Из состояния 12 следуют состояния 22, 11, 12. Из состояния 21 следуют состояния 22, 21. Из состояния 11 следуют состояния 11, 21, 12. Если же известны операторы, неопределенность только в одном месте. Из состояния 11 при операторе 44 следуют как состояние 21, так и состояние 12.

Однозначность, как меру ограничения разнообразия, можно оценить: сумма всех возможных однозначных переходов без учета неизвестного состояния NaN отнесем к всем случившимся переходам. Тогда с учетом знания об операторах коэффициент однозначности примет значение: k=13/(13+1). Если же операторы не учитывать, то k=4/(4+3+2+3). В первом случае коэффициент почти равен 1, что характеризует это преобразование как высоко предсказуемое.
А как оценить предполагаемый выигрыш в битах? Если допустить, что первоначально были неизвестны переходы между состояниями, то из каждого состояния могли бы следовать все четыре состояния. Тогда энтропия была бы равна -log(4/(4+4+4+4)). Для преобразования выше без учета операторов и без NaN уже меньше -log(4/(4+3+2+3)), а с учетом операторов -log(13/(13+1)). Если же первоначально все, включая операторы, рассматривать как состояния, то энтропия значительна -log(8/64). Можно сказать, что последовательность исследования, выраженная в битах, будет: -log(1/8), -log(1/4), -log(1/3), -log(13/14).
Код программы, который сам ищет такое преобразование, понижая неопределенность с -log(1/8) до -log(13/14), в статье не приводится.
Описана только общая логика и она такова, что
Рассматривается множество элементов {55, 54, 45, 44, 22, 12, 21, 11}.
Выдвигаются гипотезы. Берется множество операторов и множество состояний. Записываются переходы между состояниями. Например, ими могут быть: множество операторов {54, 44, 22, 21}, множество состояний {55, 45, 11}. Или как на рисунке: множество операторов {55, 54, 45, 44}, множество состояний {22, 12, 21, 11}.
Цель – максимизировать коэффициент однозначности.
В реальном мире все сложней. Мы не знаем заранее какие состояния, и какие операторы рассматривать. Наш внутренний учитель в этом случае — то, что сопротивляется энтропии, сопротивляется неопределенности потока данных, обнаруживая преобразования, имеющие предсказательную силу.
Как правило, физические законы имеют коэффициент однозначности единицу. Но выявлять и запоминать только такое — значит лишать себя возможности действовать в мире, где эта неопределенность все же присутствует и ее нельзя свести к нулю. Нужен разумный компромисс между 100% предсказуемостью и возможностью действовать, пусть и с ошибками.
Сделав это фундаментальное допущение, посмотрим на мир с точки зрения его имитации. Речь идет о компьютерных играх. Интересны они тем, что число степеней свободы несоизмеримо в них меньше. И тем интересны, что непонятно первоначально как поступать, чтобы добиться цели. Да и сама цель часто не ясна. Что же составляет их сюжетную линию, мозг как всей игры, так и отдельных персонажей? Конечные автоматы [2]. По ссылке на рисунке состояния отмечены кружками, а операторы подписаны стрелками. Это тоже преобразование. Причем с коэффициентом однозначности единица.
Итак, как мы должны поступать, если конечная цель-состояние не известна, а операторы определены? Ответ: Q-learning. Представим комнату, разбитую на множество состояний-квадратов. Где-то находится клад. Сначала мы просто передвигаемся случайно или по принципу иди туда, где меньше всего был [3]. Рано или поздно мы получим вознаграждение в виде найденного клада. В этом случае пометим целевое состояние некоторым положительным числом. В следующий раз при очередных блужданиях по комнате и находясь уже рядом с целью, отметим состояние, ведущее к цели с учетом дисконтирования. Обычно множитель берется немного меньше единицы. Но для наглядности пусть будет вычитание единицы. Так постепенно информация о цели будет распространяться на соседние и все более удаленные состояния. Можно это представить так, что вначале имеем ровную поверхность, а после многочисленного прохождения представляющей точкой по комнате, она создаст в памяти топографическую карту. И на этой карте самой высокой точкой будет сама цель. И правило, по которому оптимально нужно перемещаться к цели — двигаться в сторону возрастания числа, то есть выбирать то соседнее состояние, где оно максимально (в сторону градиента).
Допустим, у нас есть преобразование-комната, такая что состояниями ее будут {54, 61, 62, 63}, а возможными операторами {37, 38, 39}.

Пусть представляющая точка перемещается случайно в смысле выбора операторов. Если клад является состоянием 63, то информация об этом в таблице Q-learning будет постепенно распространяться на соседние состояния. Пусть наградой за клад будет число пять. Тогда с учетом дисконтирования соседние с ней состояния будут отмечены как четыре. Таковым здесь только состояние 61, из которого цель непосредственно достижима. Состояние же 62 можно получить из состояния 54.
Если состояние 54 является открытой дверью (начальным состоянием) комнаты, то оптимальный маршрут к кладу, например, может быть таким: 62=39(54) 61=37(62) 63=37(61)
Есть ли возможность разные преобразования соединить? Да. Наш язык этим и занимается. Есть языки, в которых синтаксис предложения строится за счет окончаний. Есть те, где эта роль отводится предлогам. Но это не принципиально. Существенно другое.
Базовые случаи соединения преобразований:
Преобразование А изменяет состояния преобразования В. Это возможно, если состояния преобразования А являются операторами преобразования В.
Значение переменной (то есть имя преобразования А) является значением представляющей точки этого преобразования А. И оно подставляется в качестве состояния (или оператора) в вышестоящее по иерархии преобразование С.
Что характеризует родительный падеж? Отношение принадлежности. Для примера выше: клад комнаты. Иначе говоря, одним из состояний комнаты является клад. Что соответствует второму типу соединения. В свою очередь клад может быть описан как преобразование. А комната как состояние дома. Вот что пишет Турчин [4]:

Что это значит? Что если раз за разом переходы преобразования (с учетом заданного коэффициента однозначности) именно таковы, то выносится решение (для примера выше): комната. В противном случае ее нельзя считать таковой. Далее эта информация поднимается на более высокую ступень иерархии преобразований.
Классификаторами-преобразователями могут быть что угодно. Например, ими могут быть: классификатор края изображения, классификатор движения. С обычных позиций они — фильтры для стоящий выше преобразований.
Эволюция и мышление суть схожи. Разница лишь скорости обработки информации. Цитируем Турчина [4]
Доказав свою полезность для животного, классификаторы первого уровня прочно входят в число его средств борьбы за существование. Тогда начинается следующая серия проб и ошибок: небольшое число классификаторов первого уровня (точнее, их выходных подсистем) связывается между собой в один пробный классификатор второго уровня, пока не получится полезное соединение. Затем оказывается полезным размножение этого соединения. Можно предположить, что на втором уровне иерархии — поскольку это касается органов зрения — появляются такие понятия, как граница между светом и тенью, средняя освещенность пятна, движение границы между светом и тенью и т. п. Таким же путем возникают и следующие уровни иерархии.
Вернемся к игре. Пусть имеется поток данных. Пусть он будет таким: {15, 32, 53, 41, 36, 44}, {14, 32, 36, 41}, {15, 31, 53, 34, 44}… Что можно сказать? Практически ничего. Вот с таким вот хаосом встречается и ребенок, рождаясь на свет. И только потом он начинает видеть предметы. Сначала вблизи, маму. Потом уже все знать о друге, что в соседнем подъезде. … Самое сложное — это подобрать множество операторов и множество состояний таких, что они дадут преобразование, однозначность которого не ниже заданного.
Пусть первая гипотеза такова, что множество операторов {41, 44, 45} и множество состояний {11, 12, 14, 15}. Записываем переходы. Если однозначность низкая, то гипотеза не верна. Допускаем далее, что операторами будут {11, 12, 14, 15}, а состояниями {41, 44, 45}. Если результат тоже отрицательный, то ищем иные варианты. Пусть приходим к заключению, что операторы {31, 32}, а состояния {11, 12, 14. 15}.
Мысленно усложним. Пусть состояние 11 — это преобразование, переходы которого таковы: 45=35(45) 45=35(44) 41=35(41) 44=36(45) 41=36(44) 44=36(41) 45=34(45) 44=34(44) 41=34(41). В этом случае вместо состояния 11 будем наблюдать сменяющиеся состояния {45, 44, 41}. Причем будем иметь аномалию неоднозначности преобразования в переходе из состояния 12 при операторе 32: 45|44|41=32(12). Действуем далее по принципу: где неоднозначность, там и пища (в смысле удовольствия от новизны), если из нее можно получить информацию. В том смысле, что получено преобразование с высокой предсказуемостью и логарифм от коэффициента однозначности стремится, с учетом заданной погрешности, к нулю. Поскольку преобразование 11 теперь однозначно, можно уже подставить его в вышестоящее преобразование.
Если оценить полученную информацию как разницу энтропий всей игры, то получим приблизительно: -log(1/22) - 0. Когда все переходы будут выявлены, то энтропия игры будет иметь значение ноль, а коэффициент однозначности каждого преобразования будет равен единице. Кроме того, будет известно, как соединены преобразования между собой.
Немного очеловечим рассуждения. Пусть преобразование 11 — это ключ. А преобразование выше по иерархии — лабиринт. Пусть также в лабиринте есть еще одна аномалия неоднозначности — дверь. Причем состояния преобразования ключ являются операторами преобразования дверь.
Итак, смысл всего:
Выдвигаем гипотезы, то есть берем множество операторов и множество состояний. Проверяем на однозначность.
Если преобразование удовлетворяет требуемой точности, то прогоняем ее на Q-learning, составляя топологическую карту цели. Это можно делать даже параллельно.
Способы соединения преобразований, задающие структуру предложения – это синтаксис языка. Где базовыми случаями, если не считать именительный падеж, являются винительный и родительный.
Конкретно нашей игры, последовательно решаем проблемы: не размеченный поток данных, обнаружение преобразования ключ и преобразования дверь, после этого лабиринт тоже можно считать преобразованием с заданной точностью, ключ отрывает дверь, представляющая точка из лабиринта через открытую дверь перемещается в комнату. Там она находит клад. Далее информация распространяется обратно. Чтобы найти клад комнаты, нужно предварительно открыть дверь. Дверь открывается ключом. Дверь и ключ в лабиринте. Немного упростим сказанное: ключ лабиринта, дверь лабиринта, ключ открывает дверь, открытая дверь лабиринта — открытая дверь комнаты, клад комнаты. Ниже сами преобразования и их соединения на примере игры поиска клада
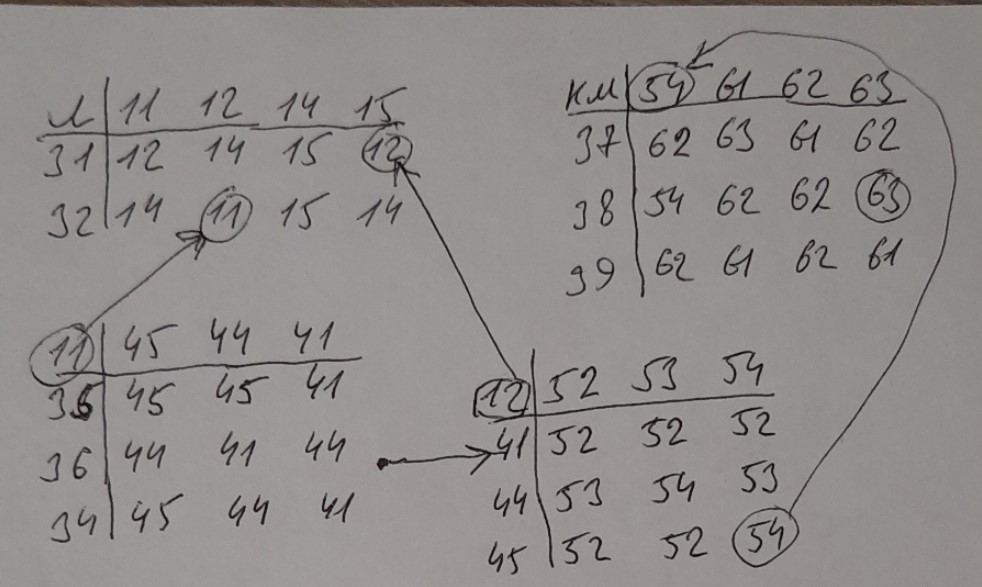
Всегда ли направление исследования должно идти от низших ступеней иерархии к высшим? Нет, конечно. Если имеем неопределенность 45|44|41=32(12), то можно, не описывая 11 как преобразование в однозначных переходах, сделать гомоморфную замену: 11=g11(45|44|41). То есть сказать: если 45, то только 11; если 44, то только 11; если 41, то только 11. Аналогично для двери: 12=g12(52|53|54). Такой подход не позволит, разумеется, однозначно предсказать состояния преобразований ключ и дверь. Но имеет то преимущество, что выразит преобразование лабиринт сразу как однозначное. Задача же определения состояний 11 и 12, как однозначных преобразований, откладывается на потом. Когда количество элементов входящего разнообразия велико, это может быть очень ценно, поскольку немедленно дает возможность ориентироваться хотя бы в части поступающего разнообразия.
Допустим, все преобразования найдены и выявлены их типы соединения. Допустим также, что текущими состояниями являются: состояние 15 лабиринта, состояние 41 ключа, состояние 52 двери.
Тогда маршрут к кладу может быть таким:
Двигаемся в лабиринте от состояния 15 к состоянию 11, то есть к ключу: 12=31(15) 11=32(12)
Меняем состояние ключа, так чтобы состояние преобразования 12 (дверь) стало 54 (открыта): 44=36(41) 44=34(44) 45=35(44) 45=35(45); при этом сама дверь перейдет от состояния 52 к 54: 52=41(52) 53=44(52) 54=44(53) 54=45(54).
В лабиринте из состояния 11 переходим к состоянию 12 (к двери): 12=31(11)
Поскольку преобразование 12 (дверь) находится в состоянии открыта, то есть в состоянии 54, то представляющая точка может двигаться из лабиринта в комнату. И уже в комнате от состояния 54 к состоянию 63 (клад).
Замечание. Вопросы синхронизации между преобразованиями здесь не оговаривались.
Немного еще гуманитарных свидетельств. Первая колонка из воспоминаний слепоглухонемой [5]. Вторая — из наблюдений за внучкой одноклассницы. Третья — опыт обучения языку жестов обезьян [6]. Комментарии. Постоянно идет специализация понятий-преобразований (стакан / вода). Что можно считать глаголом? Смену состояний, как смену кадров в кинопленке, ведущую к цели. Аня рукой бабушки гладит кошку — Аня управляет рукой бабушки, бабушка гладит кошку. Рука одноклассницы выступает в роли как управляющего, так и управляемого преобразования. Иначе говоря, рука бабушки как преобразование находится в творительном падеже.

Для тех существ, которые только начинают осваивать язык, характерно: выявление преобразования с учетом коэффициента однозначности, получение состояния в нем, включение преобразований в иерархию, обнаружение зависимости преобразований.
Литература
Эшби Р. Введение в кибернетику – М.: Прогресс, 1968
Корчаг А. Конечные автоматы и глубокое обучение в несколько строк URL
Булыгина А. В. Способы нахождения цели. Роль случайности URL
Турчин В.Ф. Феномен науки. Кибернетический подход к эволюции. URL
Келлер Х. История моей жизни URL
Смирнова А. Зорина З. О чем рассказали говорящие обезьяны: Способны ли высшие животные оперировать символами? URL
P.S. Пишите bvv2311@mail.ru