Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
Мне очень понравился разбор задачи от 3Blue1Brown, выкладываю конспект для тех, кто любит изящные решения математических задач в читабельном виде.
Длится олимпиада два раза по 3 часа, всего 12 задач по 10 баллов за каждую. Средний балл, который набирают студенты — 1 или 2. Рассмотрим одну из самых сложных задач из этой олимпиады.
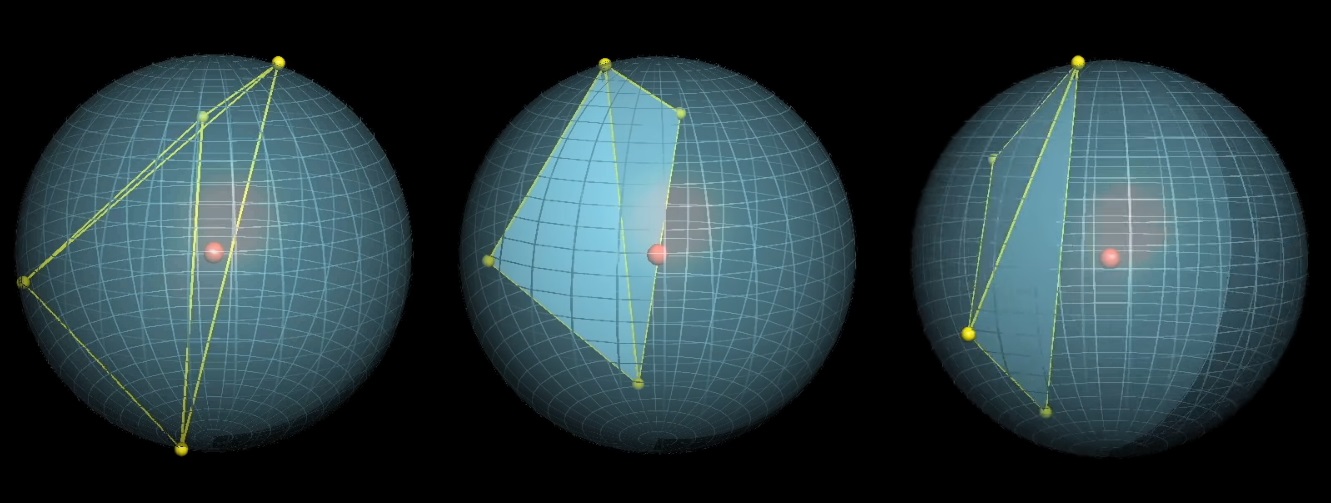
Выберем 4 случайные точки на сфере. Какова вероятность что центр сферы будет внутри тетраэдра, образованного этими точками?
Рассмотрим двумерный вариант этой задачи.
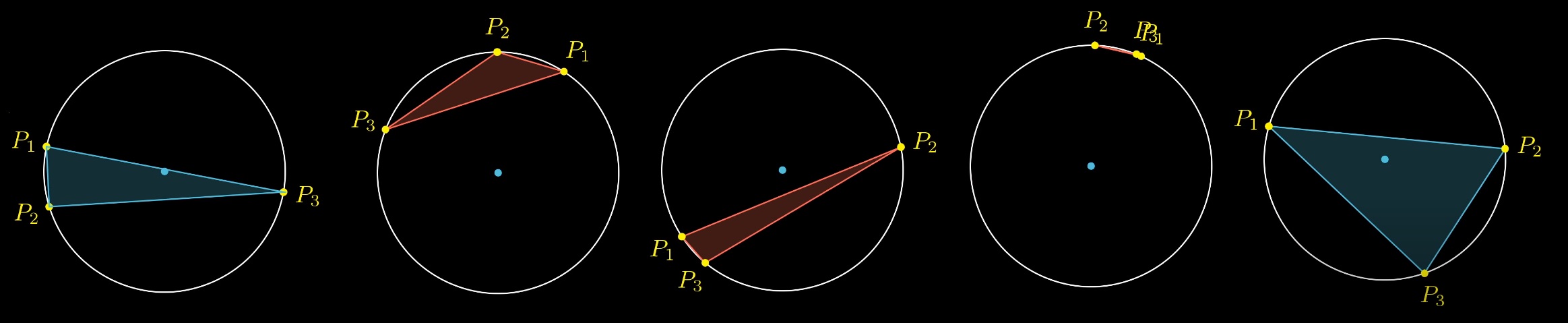
Рассмотрим 3 случайные точки на окружности. Какова вероятность, что центр окружности будет внутри треугольника?

Можно закрепить две точки и поиграться с третьей. Легко заметить, что есть определенная зона, проекции закрепленных точек относительно центра, внутрь которой должна попасть третья точка, чтобы выполнилось условие. Окружность тем самым разделяется на 4 части. Вероятность попадания третей точки в дугу, равна отношению длины дуги к длине окружности. Какова длина дуги?
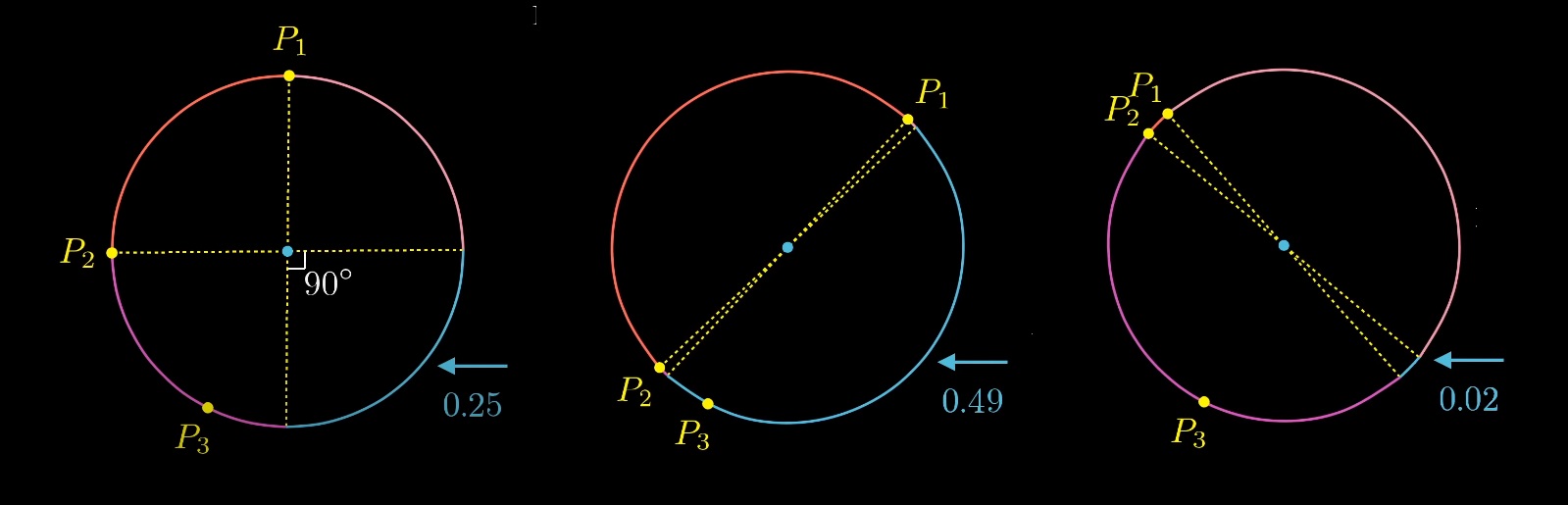
Вероятность колеблется от 0 до 0,5 в зависимости от расположения первых двух точек.
Какова средняя вероятность?

Зафиксируем первую точку и поиграемся со второй. Вероятность будет меняться от 0 до 0,5, то есть средняя вероятность будет 0,25.
Решение задачи для окружности и трёх точек — 25%.
Можно ли перенести такой подход на сферу и 4 точки?
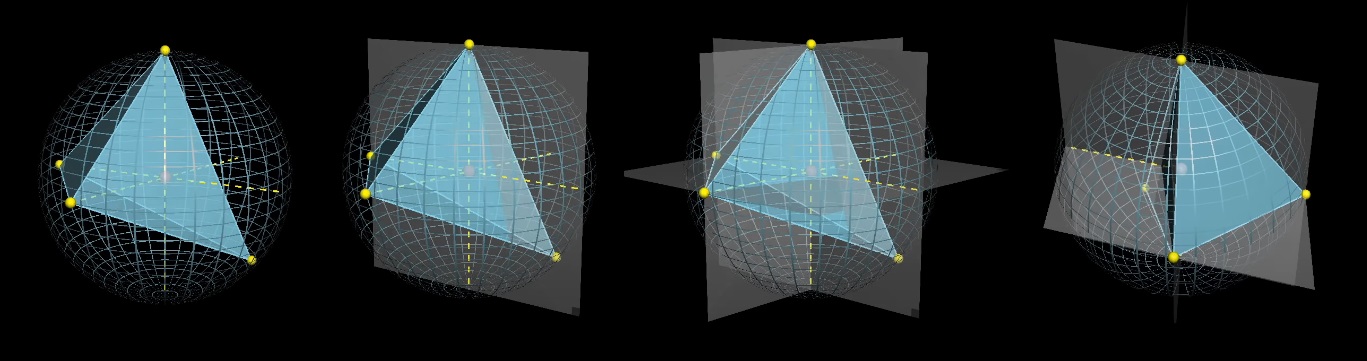
Фиксируем три точки и играем с четвертой. Нарисуем проекции фиксированных точек относительно центра и плоскостями разделим сферу на 8 частей.
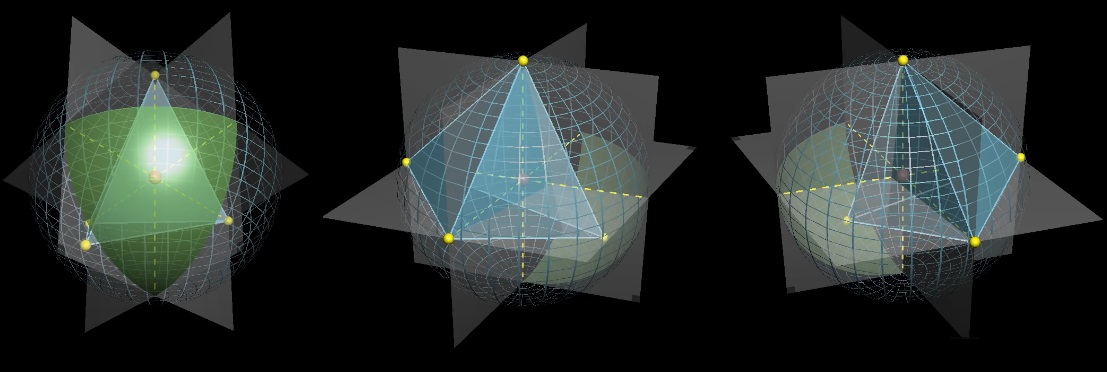
Центр сферы будет находиться внутри тетраэдра, если четвертая точка попадает на зеленый сферический треугольник, который находится «напротив» зафиксированных точек относительно центра. Каков средний размер зеленой секции?
//Дальше не придумали, импровизируй.
Можно вернуться к двумерному случаю и подумать откуда взялась 1/4. Откуда 4?
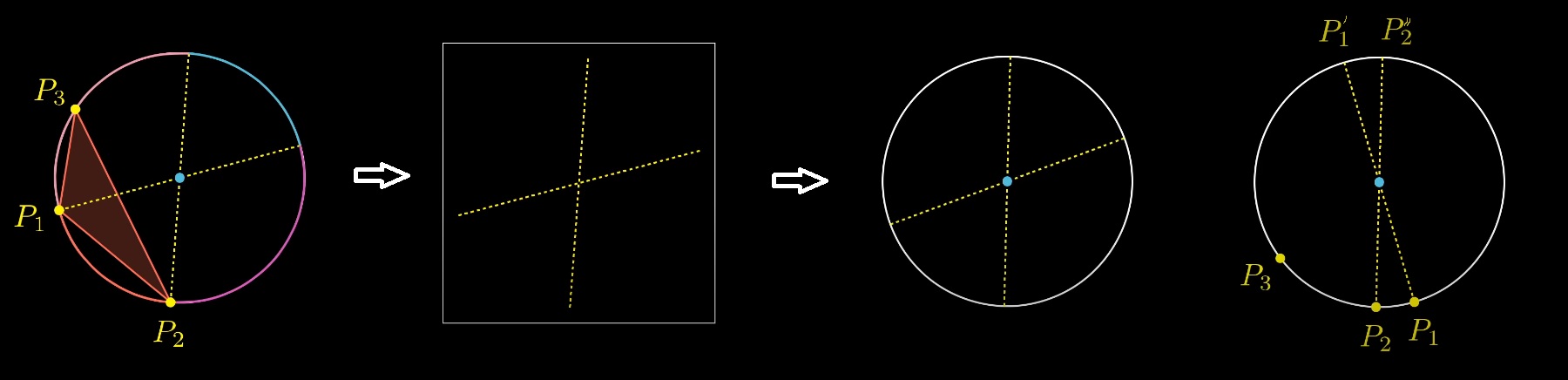
Можно перейти от 3 случайных точек на окружности к другой задаче. Выберем два случайных диаметра. Потом для каждого диаметра бросим монетку, выбирая тем самым, где будет точка Pi, с какого конца диаметра. Потом случайно выберем третью точку на окружности.
А потом еще хитрый ход.
Давайте сначала выберем случайным образом третью точку, а потом случайно выберем два диаметра. У нас будет 4 варианта размещения точек P2 P1:
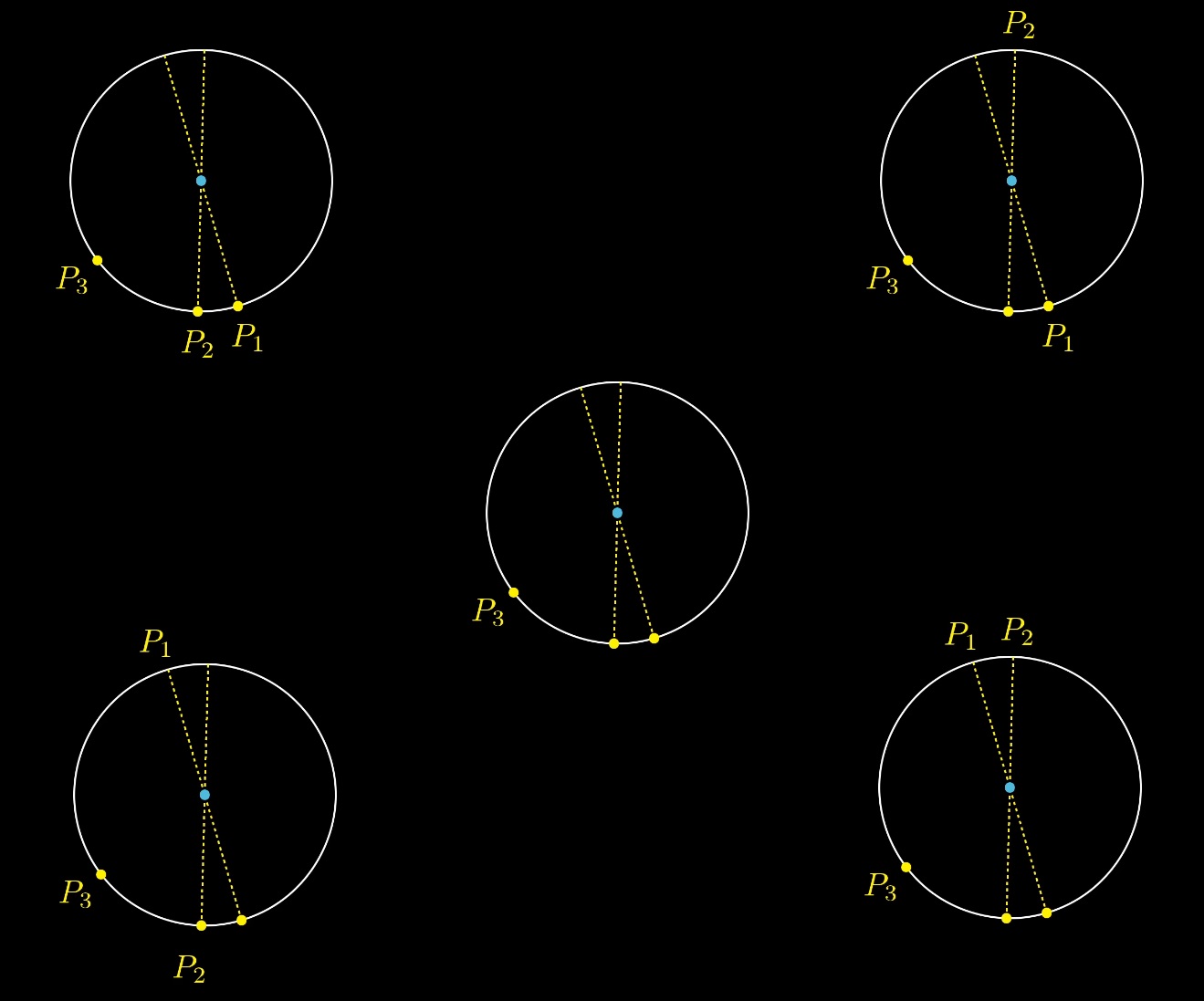
Но только один из этих 4 вариантов содержит решение, когда центр окружности внутри треугольника:
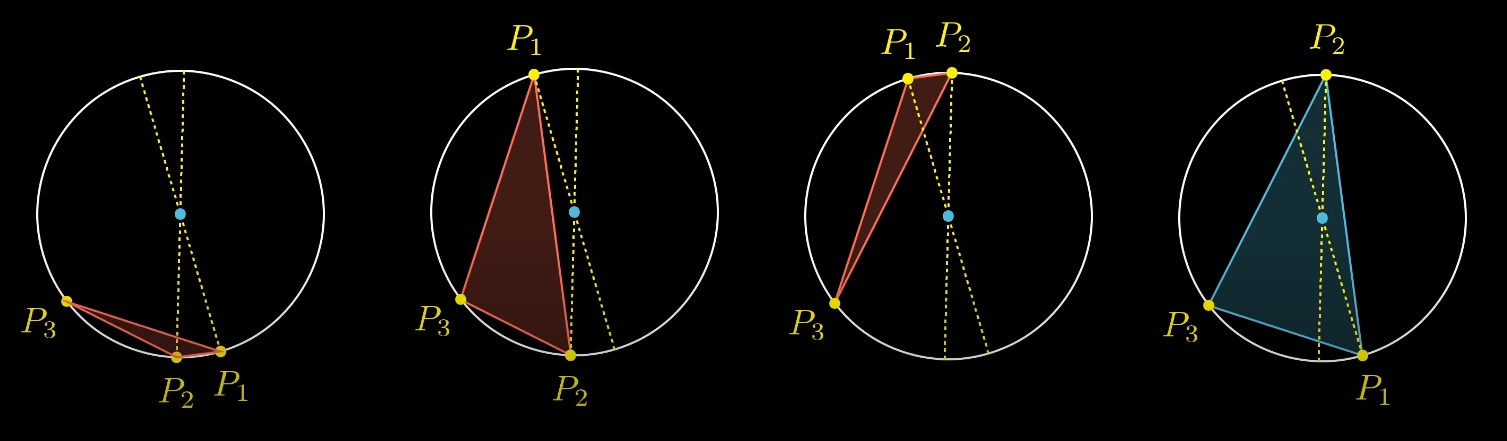
Какую бы мы ни выбирали рандомную начальную позицию третей точки и двух диаметров, только один из вариантов содержит центр окружности внутри треугольника:

То как мы переформулировали задачу:

Со сферой получается 8 вариантов выбора точек, после того, как зафиксирована первая точка и выбраны три диаметра:
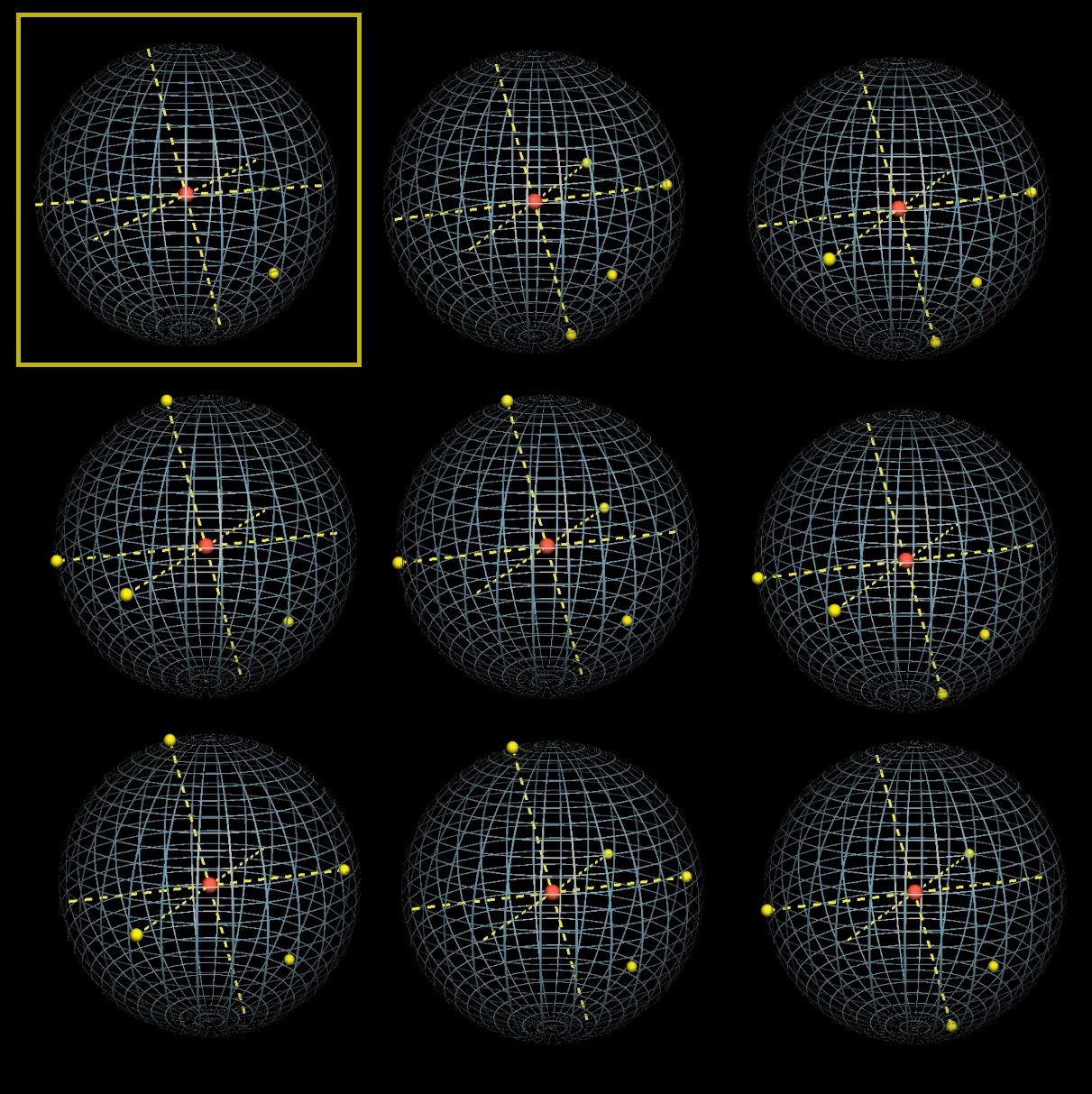
Только 1 из 8 удовлетворяет условию, что центр сферы внутри тетраэдра:
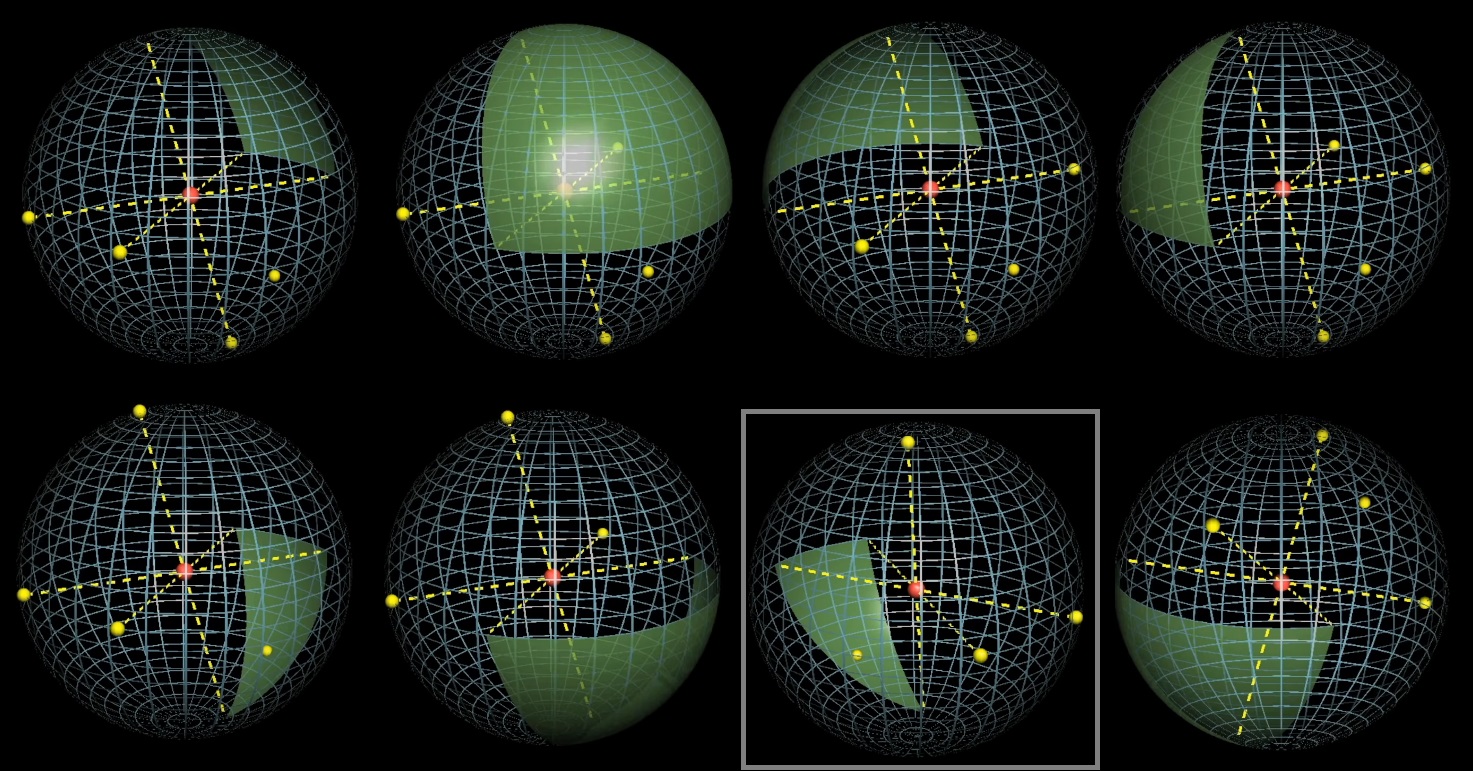
Ответ: 1/8
Математическая олимпиада им. Уильяма Лоуэлла Патнема (William Lowell Putnam Mathematical Competition) — математическая олимпиада для студентов бакалавриата, обучающихся в университетах (колледжах) США и Канады. Вдохновителем олимпиады был Уильям Лоуэлл Патнем, американский юрист и банкир. Проводится Математической ассоциацией Америки ежегодно с 1938 года. Денежными призами награждаются пять лучших университетских команд (приз $25 000 за первое место) и двадцать пять студентов, лучших в личном зачете (приз $1000 за первое место).
— Википедия
Длится олимпиада два раза по 3 часа, всего 12 задач по 10 баллов за каждую. Средний балл, который набирают студенты — 1 или 2. Рассмотрим одну из самых сложных задач из этой олимпиады.

Выберем 4 случайные точки на сфере. Какова вероятность что центр сферы будет внутри тетраэдра, образованного этими точками?
Рассмотрим двумерный вариант этой задачи.

Рассмотрим 3 случайные точки на окружности. Какова вероятность, что центр окружности будет внутри треугольника?

Можно закрепить две точки и поиграться с третьей. Легко заметить, что есть определенная зона, проекции закрепленных точек относительно центра, внутрь которой должна попасть третья точка, чтобы выполнилось условие. Окружность тем самым разделяется на 4 части. Вероятность попадания третей точки в дугу, равна отношению длины дуги к длине окружности. Какова длина дуги?

Вероятность колеблется от 0 до 0,5 в зависимости от расположения первых двух точек.
Какова средняя вероятность?

Зафиксируем первую точку и поиграемся со второй. Вероятность будет меняться от 0 до 0,5, то есть средняя вероятность будет 0,25.
Решение задачи для окружности и трёх точек — 25%.
Можно ли перенести такой подход на сферу и 4 точки?

Фиксируем три точки и играем с четвертой. Нарисуем проекции фиксированных точек относительно центра и плоскостями разделим сферу на 8 частей.

Центр сферы будет находиться внутри тетраэдра, если четвертая точка попадает на зеленый сферический треугольник, который находится «напротив» зафиксированных точек относительно центра. Каков средний размер зеленой секции?
//Дальше не придумали, импровизируй.
Можно вернуться к двумерному случаю и подумать откуда взялась 1/4. Откуда 4?

Можно перейти от 3 случайных точек на окружности к другой задаче. Выберем два случайных диаметра. Потом для каждого диаметра бросим монетку, выбирая тем самым, где будет точка Pi, с какого конца диаметра. Потом случайно выберем третью точку на окружности.
А потом еще хитрый ход.
Давайте сначала выберем случайным образом третью точку, а потом случайно выберем два диаметра. У нас будет 4 варианта размещения точек P2 P1:

Но только один из этих 4 вариантов содержит решение, когда центр окружности внутри треугольника:

Какую бы мы ни выбирали рандомную начальную позицию третей точки и двух диаметров, только один из вариантов содержит центр окружности внутри треугольника:

То как мы переформулировали задачу:

Со сферой получается 8 вариантов выбора точек, после того, как зафиксирована первая точка и выбраны три диаметра:

Только 1 из 8 удовлетворяет условию, что центр сферы внутри тетраэдра:

Ответ: 1/8
- Хардкорная линейная алгебра здесь: Capturing the Origin with Random Points: Generalizations of a Putnam Problem
- Все задачи олимпиады 1992 года: The 53rd William Lowell Putnam Mathematical Competition
Saturday, December 5, 1992





