Что? Зачем?
Всем привет!
Я хотел бы рассмотреть задачу вычислительной геометрии, а именно построение выпуклой 3D оболочки. Как мне кажется, это и не самый сложный, и не самый простой алгоритм, который было бы очень интересно и полезно разобрать.
Если Вы никогда не сталкивались с такой задачей, думаю, Вам будет интересно узнать о ней, посмотреть что это такое.
Если Вы только что-то слышали о выпуклых оболочках, Вы сможете поподробнее разузнать о них.
Если же Вы гуру выпуклых оболочек, возможно, Вам понравится еще раз послушать решение интересной задачи.
Содержание
- Что? Зачем?
- Что такое выпуклая оболочка?
- Общие слова
- Описание алгоритма
- Асимптотика
- Реализация алгоритма
- Полная реализация
Выражаю благодарность muji-4ok за помощь в написании и редактировании статьи.
Что такое выпуклая оболочка?
Выпуклой оболочкой множества X называется наименьшее выпуклое множество, содержащее множество X.
Строго, но не очень понятно. Сейчас попробую рассказать на примере:
Представим множество точек на плоскости, и, допустим, мы хотим узнать, какое минимальное количество точек надо соединить, чтобы всё оставшееся множество точек лежало внутри обведённой поверхности. Это и есть задача поиска минимальной выпуклой оболочки.

На картинке красной линией показана выпуклая 2D оболочка
Как мы видим, многие точки не входят в оболочку
Если мы поняли, что означает выпуклая оболочка, мы также сразу осознаем, что нам просто необходимо научиться ее строить, ведь зная оболочку мы сможем гораздо быстрее решать многие задачи, к примеру, просто рассматривая "внешние" точки оболочки, не обращая внимания на все точки внутри.
Общие слова
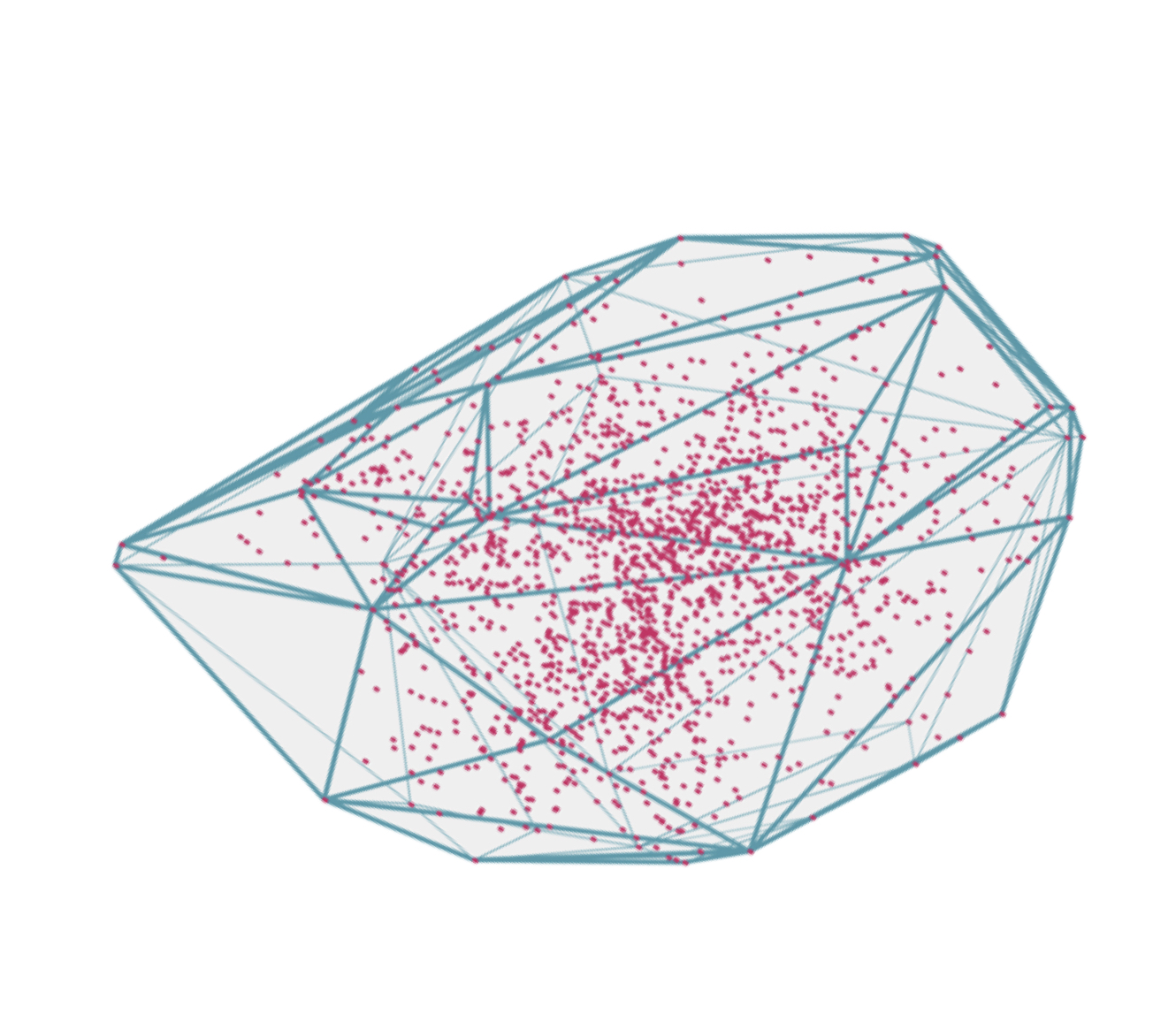
В данной статье мы будем рассматривать более сложную, чем на картинке, выпуклую оболочку, а точнее 3D оболочку. То есть наши точки будут располагаться в трехмерном пространстве, а наша оболочка будет объемной.
В связи с этим возникает вопрос: если соединение точек на плоскости нам довольно понятно и привычно, что же мы будем делать в объёмном случае?
Ответ простой — мы будем покрывать наше множество плоскостями.
Если пока не очень понятно что мы будем делать и как — так и должно быть. Пока можно представить, что у нас есть объёмный многогранник, и перед нами стоит задача: обернуть многогранник бумагой.
Вместо многогранника возьмем подарок и будем его обертывать подарочной, блестящей, бумагой.
Теперь мы можем понять, почему один из алгоритмов (который мы и будем рассматривать) поиска выпуклой оболочки называется "завертывание подарка".
Замечание Алгоритм работает только если на вход подается множество точек, в котором никакие 4 не лежат в одной плоскости. То есть каждые 3 точки задают свою плоскость.
Описание алгоритма
В алгоритме будет несколько важных этапов, поэтому мы разобьем наше построение на меньшие подзадачи, и будем поочередно их решать.
Я прошу не обращать внимание на то, что получается так много текста, это сделано для упрощения понимания 3d манипуляций, каждый пункт расписывается очень подробно. На самом деле, каждый шаг достаточно интуитивен и несложен.
1. Инициализация
Нам необходимо найти грань, с которой начнется наш алгоритм, и, в отличии от последующих действий, первую сторону мы должны найти вручную.
Это уже непростая задача, и мы попробуем максимально подробно ее объяснить.
Первую точку мы выбираем минимальную по оси Z. Понятно, что можно было бы взять любую ось, но как бы "класть" наш подарок на минимальную точку по оси Z звучит интуитивно понятнее всего. То есть в нашем воображении координатная плоскость XY сместилась, и теперь находится на одном уровне с нашей точкой. Мы как бы положили подарок на стол. Очевидно, что найденная точка будет лежать в выпуклой оболочке. Назовем первую точку P, а плоскость, на которую мы "поставили" подарок — f.
Выбор второй точки посложнее, но все еще понятен. Мы берем точку Q, находим ее проекцию на плоскость f (точку prQ). Ищем такую точку, что угол между векторами (ориентированными) {P, Q} и {Q, prQ} минимальный — то есть отмеченный на картинке угол — наибольший. Так как треугольник будет максимально тупой, значит точка Q как бы будет лежать ниже всех остальных, если смотреть по полярному углу. Поэтому точка Q тоже всегда будет лежать в выпуклой оболочке.

Выбор третьей точки совсем интересен. Мы выбираем точку R, такую что нормаль к поверхности, образуемой P, Q и R будет образовывать с вектором (0, 0, 1) минимальный угол. То есть это поверхность, максимально приближенная к плоскости f — стремится к параллельной координатной плоскости XY. Как мне кажется, картинка с таким чертежом может только ухудшить понимание, поэтому лучше попробовать понять это без углубления в картинку. Очевидно, это будет наша нижняя плоскость, а значит точка R тоже будет лежать в выпуклой оболочке.
Для дальнейшего использования алгоритма, нам потребуется хранить векторы нормали к плоскости, и так как они ориентированы, возьмем за правило брать тот вектор, который смотрит наружу (для первой грани наш вектор смотрит куда-то вниз).
Также для удобства сделаем из нашей тройки точек левую тройку векторов, то есть просто расположим точки P, Q, R по часовой стрелке.
Та-дам! Инициализация закончилась, приступаем к добавлению граней.
2. Итеративное рассмотрение ребер
Как мне кажется, вторая, и последняя, часть алгоритма проще первой. То есть если Вы поняли идею инициализации, Вам будет довольно просто понять дальнейшее добавление ребер.
Идея: Мы храним ребра в стеке, поочередно достаем их и рассматриваем: нужно ли добавить это ребро в нашу оболочку. Если надо, то мы добавляем новую грань (которая прилегает к этому ребру), а потом при необходимости добавляем в стек два ребра, которые опоясывают нашу грань. Естественно, мы смотрим, лежат ли наши ребра в нашей оболочке, и если да, то мы не добавляем их в стек.
Зам1. Как мы выбираем нужную точку? Мы помним, что хотим хранить нормали к каждой добавленной поверхности. Настало время их использовать. На определенной итерации из стека было взято ребро E. Мы смотрим на все точки, кроме точек плоскости, в которой лежит ребро E — допустим рассматриваем точку R. И смотрим на угол между нормалями к плоскости грани (в которой уже лежит ребро E) и к плоскости, образованной ребром E и точкой R. Мы помним, что наши нормали смотрят во внешнюю сторону от оболочки, то есть мы выбираем грань, которая будет максимально внешней — а именно такая и лежит в выпуклой оболочке.
Зам2. Как мы поняли из предыдущего замечания, нам необходимо находить нормали, "смотрящие во внешнюю сторону", а значит когда мы добавляем ребро E в оболочку, мы добавляем его так, чтобы точки в ребре E находились по часовой стрелке.
Зам3. Как мы помним из идеи, Мы обязаны смотреть, нужно ли добавлять ребра. То есть мы точно добавляем грань, а вот одно, или оба ребра мы можем и не добавить. Мы должны проверить, лежит ли наше ребро в оболочке, и если лежит, не добавлять.
Зам4. Если мы достали ребро, значит уже одна грань прилежит к этому ребру. Но мы точно знаем, что к одному ребру может прилежать только два ребра в выпуклой оболочке. Именно поэтому после использования этого ребра, мы обязаны "закрыть" его, чтобы дальше к нему не прибавить ни одну грань.
Зам5. Если ребро помечено, как "закрытое" мы не должны ничего с ним делать, просто переходим к следующей итерации.
Если мы соблюли все пункты этого алгоритма, по выходе из стека (когда он станет пуст), мы построили нашу минимальную выпуклую 3D оболочку.
Асимптотика
Перед тем, как приступить к реализации алгоритма, давайте подумаем над его асимптотикой. Мы рассматриваем каждое ребро выпуклой оболочки, а затем смотрим на все точки нашего множества. Поэтому если мощность множества N, а в нашей оболочке H ребер, сложность алгоритма O(NH). В худшем случае H вырождается в 2N, и тогда алгоритм работает за O(N^2).
Возможно, это не лучшая асимптотика, ведь есть алгоритм Чана, работающий за O(NlogN), но лично мне кажется, что завертывание подарка лучше иллюстрирует сам процесс построения выпуклой оболочки. Хотя если мы вспомним построение 2D оболочки, которая довольно просто строится за O(NlogN), мы понимаем, что хоть мы и переходим в трехмерное измерение, и все вычисление становятся гораздо сложнее и непонятнее, по асимптотике мы ушли не так далеко.
А теперь, пожалуй, мы пришли к самому интересному: реализация алгоритма.
Реализация алгоритма
Я постараюсь разбивать код на максимально мелкие части и объяснять смысл последовательно, тем не менее, некоторые части разбить не получится, и будет достаточно большой, хоть и не сложный, но сплошной код. В конце приведена полная реализация алгоритма на C++.
Хранение точек. Мы будем хранить точки в структуре. Важно понимать, что зачастую, вместо точек мы будем подразумевать радиус-вектора. Как и у радиус-вектора у точки будут определены простейшие операторы. (для просмотра полной реализации, спуститесь в конец).
struct Point
{
coordinate x;
coordinate y;
coordinate z;
Point (coordinate x = 0, coordinate y = 0, coordinate z = 0) : x(x), y(y), z(z) {}
Point operator- (const Point& other) const;
Point operator+ (const Point& other) const;
bool operator!= (const Point& other) const;
bool operator== (const Point& other) const;
};Функции подсчета. Нам нужно уметь вычислять определители матриц 2х2 для дальнейшего подсчета векторного произведения (для нахождения нормалей).
coordinate Det2x2(coordinate a11, coordinate a12, coordinate a21, coordinate a22)
{
return a11 * a22 - a12 * a21;
}Соответственно нужно уметь считать само векторное произведение (где точка A — стартовая — или по-другому точка начала координат для двух радиус-векторов AB и AC):
Point VectorProduct(const Point& A, const Point& B, const Point& C)
{
Point a = B - A;
Point b = C - A;
return Point (Det2x2(a.y, a.z, b.y, b.z),
Det2x2(a.x, a.z, b.x, b.z),
Det2x2(a.x, a.y, b.x, b.y));
}Нужно уметь находить длину вектора (для нормализации и нахождения углов):
double GetLenghtVector(Point A, Point B = Point(0, 0, 0))
{
Point vec = B - A;
double lenght = std::sqrt(vec.x * vec.x + vec.y * vec.y + vec.z * vec.z);
return lenght;
}Ну и конечно нужно находить угол между двумя векторами:
double GetAngle(const Point& n1, const Point& n2)
{
double len_n1 = GetLenghtVector(n1);
double len_n2 = GetLenghtVector(n2);
double scalar_prod = n1.x * n2.x + n1.y * n2.y + n1.z * n2.z;
if (scalar_prod == 0)
{
return 0;
}
return std::acos((scalar_prod) / (len_n1 * len_n2));
}На этом малосодержательная и техническая часть заканчивается, начинается построение минимальной выпуклой оболочки.
Грани и ребра. Мы будем хранить внутри нашей оболочки и грани, и ребра. В каждом ребре мы сохраняем номер нашей грани, ведь нам придется иногда обращаться к третьей точке нашей плоскости, также нам нужно будет знать нормаль к плоскости, в которой лежит данная точка, а ее логичнее хранить в структуре грани. Для оптимизации памяти и упрощения работы, мы будем хранить только номера наших точек, которые будут храниться в отдельном массиве.
struct Edge
{
int first;
int second;
int flatness; //номер грани
bool is_close = false; // открыто ли наше ребро, можно ли добавить еще грань?
Edge(int first, int second, int flatness = -1, Point normal = Point(0, 0 , 0)) :
first(first), second(second), flatness(flatness) {}
};Далее объявим структуру Flatness — грани нашей оболочки. Там хранится 3 точки, нормаль к поверхности (направленная вовне оболочки). А также есть специальный метод — Another, который по двум точкам плоскости находит третью. (его реализация — просто три if — можно также посмотреть в конце.)
struct Flatness
{
int first;
int second;
int third;
Point normal; // нормаль к грани, изначально содержащее это ребро
Flatness(int first, int second, int third, Point normal) :
first(first), second(second), third(third), normal(normal) {}
int Another(int one, int two);
};Class Выпуклая оболочка.
class ConvexHull
{
struct Flatness;
struct Edge;
std::vector<Point> points_; // Точки изначального множества
std::vector<Flatness> verge_; // Грани
std::vector<Edge> edges_; // Ребра
int count_; // Количество точек изначального множества
int findMinZ() const;
void findFirstFlatness();
int returnIsEdgeInHull(int a, int b) const;
void makeHull();
public:
ConvexHull(const std::vector<Point> points): points_(points), count_(points.size()) { makeHull(); }
};Вспомогательные методы
Поиск первой точки: минимальной по оси Z (для упрощения, также сортируется и по остальным координатам в обратном лексикографическом порядке)
int ConvexHull::findMinZ() const
{
int min_id = 0;
for (int i = 1; i < count_; ++i)
{
if (points_[i].z < points_[min_id].z ||
(points_[i].z == points_[min_id].z && points_[i].y < points_[min_id].y) ||
(points_[i].z == points_[min_id].z && points_[i].y == points_[min_id].y &&
points_[i].x < points_[min_id].x))
{
min_id = i;
}
}
return min_id;
}Проверка, лежит ли уже определенное определенное ребро в массиве ребер:
int ConvexHull::returnIsEdgeInHull(int a, int b) const
{
for (int i = 0; i < edges_.size(); ++i)
{
if ((edges_[i].first == a && edges_[i].second == b) ||
(edges_[i].first == b && edges_[i].second == a))
{
return i;
}
}
return -1;
}Сам алгоритм. (наконец-то)
Теперь поочередно будем смотреть на стадии работы алгоритма. Напомню, их две основных: инициализация и итеративное построение. Если кто-то не прочитал еще описание алгоритма, настоятельно рекомендую это сделать, ведь я буду опираться на данную там информацию.
Шаг первый:
void ConvexHull::findFirstFlatness()
{
int first_point, second_point, third_point; // наши первые три точки
first_point = findMinZ();сейчас мы нашли первую точку, как минимальную по оси Z. Именно на эту точку мы будем класть наш "подарок".
double min_angle = 7; // Так как угол может быть от нуля до 2pi, он никогда не будет больше 7
int min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i) // наша вторая точка не должна совпадать с первой
{
continue;
}
Point start = points_[first_point];
Point next = points_[i];
double angle = GetAngle(start - next, next - Point(next.x, next.y, start.z));
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
second_point = min_id;В этой части мы нашли вторую точку, как минимальное отклонение от плоскости основания.
min_angle = 7;
min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i || second_point == i)
{
continue;
}
Point normal = VectorProduct(points_[first_point], points_[second_point], points_[i]);
double angle = GetAngle(Point(0, 0, 1), normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
third_point = min_id;Третью точку мы находим такую, чтобы плоскость, проходящая через первые две и искомую точку была максимальна приближена к координатной плоскости XY, у которой нормаль (0, 0, 1). Что и отражено в поиске нашего угла.
И в конце мы должны правильно ориентировать наши три точки (как левая тройка векторов), добавить нулевую грань и правильно добавить наши три ребра в вектор ребер.
if (VectorProduct(points_[first_point], points_[second_point], points_[third_point]).z > 0)
{
std::swap (second_point, third_point);
}
Point new_normal = VectorProduct(points_[first_point], points_[second_point], points_[third_point]);
verge_.push_back(Flatness(first_point, second_point, third_point, new_normal)); // нулевая грань
edges_.push_back(Edge(first_point, second_point, 0));
edges_.push_back(Edge(second_point, third_point, 0));
edges_.push_back(Edge(third_point, first_point, 0));
}Шаг второй:
Начинаем с вызова нашей функции инициализации и со скучного добавления первых ребер:
void ConvexHull::makeHull()
{
findFirstFlatness();
std::stack<int> stack;
stack.push(0);
stack.push(1);
stack.push(2);А вот теперь сердце нашего алгоритма: наш цикл, пока стек не пуст. Так как это единый блок, я разобью код всего на две части: нахождение точки и проверка ее корректности и добавление ребер в массив.
while (!stack.empty())
{
Point new_normal;
Edge e = edges_[stack.top()]; // берем верхнее ребро, рассматриваем его
stack.pop();
if (e.is_close) // если в ребро уже нельзя добавлять грани, мы этого не делаем
{
continue;
}
int min_id = -1;
double min_angle = 7;
for (int i = 0; i < count_; ++i)
{
int another = verge_[e.flatness].Another(e.first, e.second);
if (i != another && e.first != i && e.second != i) // проверка, что точка не из той же грани
{
// нахождение нормали к плоскости, образуемой ребром и i-ой точкой
Point current_normal = VectorProduct(points_[e.second], points_[e.first], points_[i]);
double angle = GetAngle(current_normal, verge_[e.flatness].normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
new_normal = current_normal;
}
}
}Соответственно после нахождения такой точки надо проверить, есть ли уже ребра, ведущие из ребра e в найденную вершину, и при необходимости запомнить. Также если мы не добавляем ребро, то есть такое ребро уже присутствует в оболочке, мы красим его в is_closed = true, ведь мы в любом случае добавляем грань, даже если это ребро уже есть в оболочке, а значит, к данному ребру будет примыкать два ребра — максимальное количество — наше добавленное и то, которое и добавило ребро е в оболочку.
if (min_id != -1) // защита от дурака - если в оболочке меньше 4х вершин
{
e.is_close = true; // раз мы рассмоттрели это ребро, значит добавили уже вторую грань к этому ребру
int count_flatness = verge_.size(); // номер нашей грани
int first_edge_in_hull = returnIsEdgeInHull(e.first, min_id); // возвращает -1, если ребра еще нет
int second_edge_in_hull = returnIsEdgeInHull(e.second, min_id);
if (first_edge_in_hull == -1)
{
edges_.push_back(Edge(e.first, min_id, count_flatness));
stack.push(edges_.size() - 1);
}
if (second_edge_in_hull == -1)
{
edges_.push_back(Edge(min_id, e.second, count_flatness));
stack.push(edges_.size() - 1);
}
if (first_edge_in_hull != -1)
{
edges_[first_edge_in_hull].is_close = true;
}
if (second_edge_in_hull != -1)
{
edges_[second_edge_in_hull].is_close = true;
}
verge_.push_back(Flatness(e.first, e.second, min_id, new_normal));
}
} // закрытие while
} // закрытие метода#include <iostream>
#include <vector>
#include <cmath>
#include <stack>
#include <iomanip>
using coordinate = int64_t;
struct Point;
coordinate Det2x2(coordinate a11, coordinate a12, coordinate a21, coordinate a22);
Point VectorProduct(const Point& A, const Point& B, const Point& C);
double GetLenghtVector(Point A, Point B);
double GetAngle(const Point& n1, const Point& n2);
struct Point
{
coordinate x;
coordinate y;
coordinate z;
Point(coordinate x = 0, coordinate y = 0, coordinate z = 0) : x(x), y(y), z(z) {}
Point operator-(const Point& other) const
{
return Point(x - other.x, y - other.y, z - other.z);
}
Point operator+(const Point& other) const
{
return Point(x + other.x, y + other.y, z + other.z);
}
bool operator!= (const Point& other) const
{
return (x != other.x || y != other.y || z != other.z);
}
bool operator== (const Point& other) const
{
return (x == other.x && y == other.y && z == other.z);
}
};
coordinate Det2x2(coordinate a11, coordinate a12, coordinate a21, coordinate a22)
{
return a11 * a22 - a12 * a21;
}
//[AB, AC]
Point VectorProduct(const Point& A, const Point& B, const Point& C)
{
Point a = B - A;
Point b = C - A;
return Point (Det2x2(a.y, a.z, b.y, b.z),
Det2x2(a.x, a.z, b.x, b.z),
Det2x2(a.x, a.y, b.x, b.y));
}
//vector AB
double GetLenghtVector(Point A, Point B = Point(0, 0, 0))
{
Point vec = B - A;
double lenght = std::sqrt(vec.x * vec.x + vec.y * vec.y + vec.z * vec.z);
return lenght;
}
double GetAngle(const Point& n1, const Point& n2)
{
double len_n1 = GetLenghtVector(n1);
double len_n2 = GetLenghtVector(n2);
double scalar_prod = n1.x * n2.x + n1.y * n2.y + n1.z * n2.z;
if (scalar_prod == 0)
{
return 0;
}
return std::acos((scalar_prod) / (len_n1 * len_n2));
}
class ConvexHull
{
struct Flatness
{
int first;
int second;
int third;
Point normal; // нормаль к грани, изначально содержащее это ребро
Flatness(int first, int second, int third, Point normal) :
first(first), second(second), third(third), normal(normal) {}
int Another(int one, int two)
{
if ((one == first && two == second) || (one == second && two == first))
{
return third;
}
if ((one == first && two == third) || (one == third && two == first))
{
return second;
}
if ((one == third && two == second) || (one == second && two == third))
{
return first;
}
return -1; // error
}
};
struct Edge
{
int first;
int second;
int flatness; //номер грани
bool is_close = false;
Edge(int first, int second, int flatness = -1, Point normal = Point(0, 0 , 0)):
first(first), second(second), flatness(flatness) {}
};
std::vector<Point> points_;
std::vector<Flatness> verge_;
std::vector<Edge> edges_;
int count_; // Количество точек изначального множества
int findMinZ() const;
void findFirstFlatness();
int returnIsEdgeInHull(int a, int b) const;
void makeHull();
public:
ConvexHull(const std::vector<Point> points): points_(points), count_(points.size()) { makeHull();}
};
void ConvexHull::makeHull()
{
findFirstFlatness();
std::stack<int> stack;
stack.push(0);
stack.push(1);
stack.push(2);
while (!stack.empty())
{
Point new_normal;
Edge e = edges_[stack.top()]; // берем верхнее ребро, рассматриваем его
stack.pop();
if (e.is_close) // если в ребро уже нельзя добавлять грани, мы этого не делаем
{
continue;
}
int min_id = -1;
double min_angle = 7;
for (int i = 0; i < count_; ++i)
{
int another = verge_[e.flatness].Another(e.first, e.second);
if (i != another && e.first != i && e.second != i) // проверка, что точка не из той же грани
{
// нахождение нормали к плоскости, образуемой ребром и i-ой точкой
Point current_normal = VectorProduct(points_[e.second], points_[e.first], points_[i]);
double angle = GetAngle(current_normal, verge_[e.flatness].normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
new_normal = current_normal;
}
}
}
if (min_id != -1) // защита от дурака - если в оболочке меньше 4х вершин
{
e.is_close = true; // раз мы рассмоттрели это ребро, значит добавили уже вторую грань к этому ребру
int count_flatness = verge_.size(); // номер нашей грани
int first_edge_in_hull = returnIsEdgeInHull(e.first, min_id);
int second_edge_in_hull = returnIsEdgeInHull(e.second, min_id);
if (first_edge_in_hull == -1)
{
edges_.push_back(Edge(e.first, min_id, count_flatness));
stack.push(edges_.size() - 1);
}
if (second_edge_in_hull == -1)
{
edges_.push_back(Edge(min_id, e.second, count_flatness));
stack.push(edges_.size() - 1);
}
if (first_edge_in_hull != -1)
{
edges_[first_edge_in_hull].is_close = true;
}
if (second_edge_in_hull != -1)
{
edges_[second_edge_in_hull].is_close = true;
}
verge_.push_back(Flatness(e.first, e.second, min_id, new_normal));
}
} // закрытие while
} // закрытие метода
int ConvexHull::findMinZ() const
{
int min_id = 0;
for (int i = 1; i < count_; ++i)
{
if (points_[i].z < points_[min_id].z ||
(points_[i].z == points_[min_id].z && points_[i].y < points_[min_id].y) ||
(points_[i].z == points_[min_id].z && points_[i].y == points_[min_id].y &&
points_[i].x < points_[min_id].x))
{
min_id = i;
}
}
return min_id;
}
void ConvexHull::findFirstFlatness()
{
int first_point, second_point, third_point;
first_point = findMinZ();
double min_angle = 7;
int min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i)
{
continue;
}
Point start = points_[first_point];
Point next = points_[i];
double angle = GetAngle(start - next, next - Point(next.x, next.y, start.z));
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
second_point = min_id;
min_angle = 7;
min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i || second_point == i)
{
continue;
}
Point normal = VectorProduct(points_[first_point], points_[second_point], points_[i]);
double angle = GetAngle(Point(0, 0, 1), normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
third_point = min_id;
// правильное ориентирование
if (VectorProduct(points_[first_point], points_[second_point], points_[third_point]).z > 0)
{
std::swap (second_point, third_point);
}
Point new_normal = VectorProduct(points_[first_point], points_[second_point], points_[third_point]);
verge_.push_back(Flatness(first_point, second_point, third_point, new_normal)); // перая грань
edges_.push_back(Edge(first_point, second_point, 0));
edges_.push_back(Edge(second_point, third_point, 0));
edges_.push_back(Edge(third_point, first_point, 0));
}
int ConvexHull::returnIsEdgeInHull(int a, int b) const
{
for (int i = 0; i < edges_.size(); ++i)
{
if ((edges_[i].first == a && edges_[i].second == b) ||
(edges_[i].first == b && edges_[i].second == a))
{
return i;
}
}
return -1;
}Буду рад ответить на интересующие вопросы в комментариях и личных сообщениях.