В работе Индера Танежа (Inder J. Taneja) (бразильского математика-популяризатора математики) от 2014 года: Crazy Sequential Representation: Numbers from 0 to 11111 in terms of Increasing and Decreasing Orders of 1 to 9 (Сумасшедшее последовательное представление: числа от 0 до 11111 в порядке возрастания и убывания от 1 до 9).
Был один пробел, а именно число 10958, который немного всколыхнул научное сообщество, и самое главное до сих пор не заполнен. Вот про него мы и поговорим.

Для начала об самой статье Crazy Sequential Representation… В ней основная часть отведена таблице на 160 листов на которых любое число (от 0 до 11 111) приставлено операциями над двумя последовательностями чисел. Последовательности такие:
* 1, 2, 3, 4, 5, 6, 7, 8, 9
* 9, 8, 7, 6, 5, 4, 3, 2, 1
Например, 2021 представить можно так
* 2021 = 12×(3×4 + 5 + 6)×7 + 89
* 2021 = (9×8 + 7 + 6)×5×4 + 321
А 307 так:
* 307 = 123 + 45 + 67 + 8×9
* 307 = 9×8 + 7×6×5 + 4×3×2 + 1
Важно понимать, что последовательности 1, 2…8, 9 и 9, 8…2, 1 не должны нарушаться при визуальной записи. Более того, набор допустимых операций – это самый базовый «школьный» набор:
* plus (плюс);
* minus (минус);
* product (умножение);
* potentiation (возведение в степень);
* division (деление);
* brackets (скобки)
«Сложные» операции такие как — факториал, квадратный корень и т.д. недопустимы…
Самое удивительное, что все числа, до 11 111, мы можем получить благодаря этим базовым операциям… Ну или почти все… Одно число раскололо математическое сообщество на два лагеря. Это число — 10958. В статье Танежа написано так:
* 10958 = still not available (все еще недоступно)
* 10958= (9 + 8 × 7 × 65 + 4) × 3 − 2 + 1
Т.е. математики сначала загнали себе в рамки, а потом раскололись из-за рамок на два лагеря. Первые сказали — что такая последовательность базовых операций должна существовать, но еще не найдена. Вторые – нашли решение, но схитрили и расширили понятие «базовые операции».
Что бы понять «о чем спор» для начала вернемся к числу 2021 из таблицы. Сейчас это число вычисляется так:
* 2021 = 12×(3×4 + 5 + 6)×7 + 89
Как видно, здесь есть два «странных» числа – это 12 и 89, которые выбиваются из начальных условий. Ибо, из «условий задачи», начальные числа должны быть из следующего множества: 1, 2, 3, 4, 5, 6, 7, 8, 9, а тут появляются 12 и 89… Что не совсем честно… И отсюда и появляется идея у одной из групп математиков. Они ввели новую операцию – «конкатенацию» и сказали, что она «базовая»… Проблема в том, что для операции «конкатенации» даже общепринятого символа нет, а тут её решили причислить к базовым…
И раз никто не знает, как её толком обозначить, а мне статью писать нужно, в дальнейшем, операцию «конкатенации» будем обозначать символом ‖ (т.к. именно это обозначение я встречал чаще всего).
Давайте вспомним свойства конкатенации.
1) Операция конкатенации ассоциативна.
То есть, если нужно выполнить конкатенацию трёх слов, то от расстановки скобок результат не изменится: ( wiki ‖ media ) ‖ pedia = wikimediapedia, и в то же время wiki ‖ ( media ‖ pedia ) = wikimediapedia.
2) Операция конкатенации некоммутативна.
В самом деле, wiki ‖ media = wikimedia, но media ‖ wiki = mediawiki ≠ wikimedia. От перестановки операндов меняется результат операции, что и означает её некоммутативность.
3) Пустое слово — ε, — является нейтральным элементом (единицей) операции конкатенации.
То есть, если ε— пустое слово, то для любого слова α выполнено равенство: ε ‖ a = a ‖ ε = a
4) Длина (количество букв) конкатенации слов равна сумме длин операндов:
|α ‖ β| = |α| + |β|.
Эти свойства вполне себе известны и описаны на википедии.
Добавим еще описание приоритетности:
5) (плюс, минус) < (умножение, деление) < (возведение в степень) < (конкатенация)
И так. Вернемся к таблице Танежа, а именно числу 2021.
Напомню, сейчас это число записано так: 2021 = 12×(3×4 + 5 + 6)×7 + 89.
Так вот, с вводом «новой» операции, это число будет записано так:
* 2021 = (1 ‖ 2) × (3 × 4 + 5 + 6) × 7 + (8 ‖ 9).
В целом поменялся только формат записи. Всё остальное работает, как и раньше. Но фокус в том, что в таком случае, математики нашли решение для числа 10958.
* 10958 = 1 × (2‖3) + (((4 × 5 × 6) ‖ 7) + 8) × 9
Пояснение:
1 × (2‖3) + (((4 × 5 × 6) ‖ 7) + 8) × 9
= 1 × 23 + ((120 ‖ 7) + 8) × 9
= 1 × 23 + (1207 + 8) × 9
= 1 × 23 + 1215 × 9
= 23 + 10935
= 10958
И вот на этом обычно все видосики и статьи заканчиваются, показываю вот такой вот математический фокус и оставляя всех размышлять на чьей стороне зритель… А, я продолжу. Ибо фокус открывается весьма интересный пласт операций.
Начнем с того — почему эта операция вообще не нравится первой группе ученых.
Операция «конкатенация» вообще не считается арифметической операцией… Это операция склеивания объектов линейной структуры, обычно строк, что собственно и это собственно отталкивает «первую» часть математиков. Они говорят — мол, нужно делать математические операции, а не «хаки»… Поэтому я попробую перевести операцию конкатенации в алгебраическую плоскость и более того постараюсь показать, что операция вполне базовая, а потом готов выслушать ваше мнение, о том где я не прав.
В действительности все натуральные числа можно представить через операцию конкатенации: 1‖0‖9‖5‖8. И дабы показать, что эту операцию можно отнести к базовым немного попрыгаем по системам счисления.
Возьмем число 10958 в разных представлениях:
Двоичная: 10 1010 1100 1110 = 1‖0‖1‖0‖1‖0‖1‖1‖0‖0‖1‖1‖1‖0
Восьмеричная: 25316 = 2‖5‖3‖1‖6
Шестнадцатеричная 2ACE = 2‖A‖C‖E = 2‖10‖12‖14
Ого, в шестнадцатеричной система стало еще интересней, оказывается через операцию конкатенации мы можем выражать числа используя не только «хак» с буквами A, B, C, D, E, F, но и через стандартные арабские числа от 0 до 16… Хотя стоп… Сверху мы описали операцию конкатенации немного не так. Т.е. для случая 2‖10‖12‖14 мы получаем совсем другое число. Получается нам нужно поменять определение операции «конкатенации», которую мы применяем к числам, так, давайте сделаем это. Но для начала вспомним представления других операций.
Умножение можно представить как:

Возведение в степень:

Школьный курс вспомнили, теперь вспомни, что еще в школьном курсе было умножение на 10. Которое позволяло «подставлять числа сзади». Ну т.е.:
* 1‖0‖9‖5‖8 = (((1 * 10 + 0) * 10 + 9) * 10 + 5) * 10 + 8.
Итого мы разложили операцию «конкатенации» так: a ‖ b = (a * 10) + b; Но 10 — это хитрое число… Это число следующие за максимальным из группы в системе счисления, ну т.е. это просто основание системы счисления т.е. общий вид такой:
a ‖ b = (a * m) + b, где m – основание системы счисления представленное в обозначении самой системы.
Но такое определение мне не очень нравится, ибо m больше чем возможные числа внутри системы. Давайте сделаем чуть хитрее.
 ,
,
где — это целое число означающее 1 в системе счисления, а — основание системы счисления. Т.е. мы по факту складываем палочки. Вот теперь получилось красиво с точки зрения определения, но
a ‖ b = (a * 10) + b – легче для восприятия.
Давайте, на всякий случай, проверим, что действительно это работает и пересчитаем описанные выше операции на 10958.
Двоичная: 10 1010 1100 1110 = 1‖0‖1‖0‖1‖0‖1‖1‖0‖0‖1‖1‖1‖0 = ((((((((((((1 * 10 + 0) * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 1) * 10 + 0) * 10 + 0) * 10 + 1) * 10 + 1) * 10 + 1) * 10 + 0

Восьмеричная: 25316 = 2‖5‖3‖1‖6 = (((2 * 10 + 5) * 10 + 3) * 10 + 1) * 10 + 6
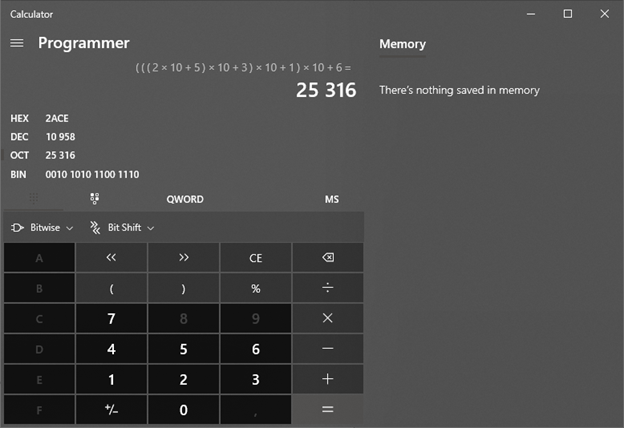
Шестнадцатеричная 2ACE = 2‖A‖C‖E = ((2 * 10 + A) * 10 + C) * 10 + E
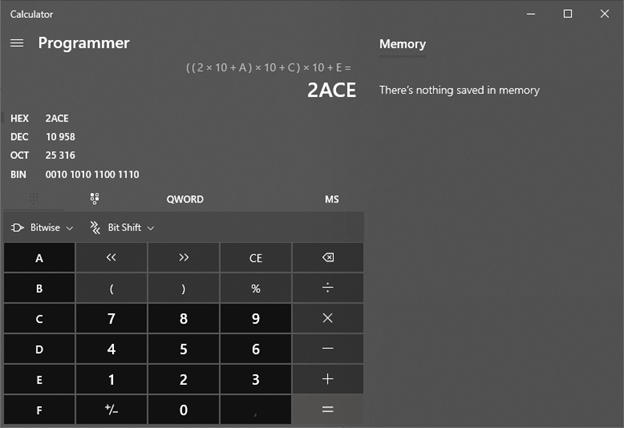
Собственно, в таком определении операции конкатенации, мы перевели её в алгебраическую плоскость. Причем свойства операции, написанные выше, сохраняются.
Получается мы решили загадку числа 10958? Ну… Давайте проверим. Получается, что мы должны изменив систему счисления получить те же данные из таблицы Танежа.
Возьмем к примеру число: 238 (в нем важно, что все числа в решении стоят отдельно), тогда получаем:
Десятичная:
238
= 1 + 2×3 + 4 + 5×6×7 + 8 + 9
= 1 + 6 + 4 + 210 + 8 + 9
= 238
Восьмеричная (т.е. 8 = 10, 9 = 11):
356
= 1 + 2×3 + 4 + 5×6×7 + 10 + 11
= 1 + 6 + 4 + 322 + 10 + 11
= 356
Шестнадцатеричная:
EE
= 1 + 2×3 + 4 + 5×6×7 + 8 + 9
= 1 + 6 + 4 + D2 + 8 + 9
= EE
В итоге мы получаем, что результат сохраняются при переводе чисел в другую систему счисления, что собственно логично и круто. А вот с введением нашей операции «конкатенации» так не получается…
Десятичная:
10958
= 1 × (2‖3) + (((4 × 5 × 6) ‖ 7) + 8) × 9
= 1 × (2 * 10 + 3) + (((4 × 5 × 6) * 10 + 7) + 8) × 9
= 1 × (2 * 10 + 3) + ((120 * 10 + 7) + 8) × 9
= 1 × (20 + 3) + ((1200 + 7) + 8) × 9
= 1 × 23 + (1207 + 8) × 9
= 1 × 23 + 1215 × 9
= 23 + 10935
= 10958
Восьмеричная (т.е. 8 = 10, 9 = 11):
25316
= 1 × (2‖3) + (((4 × 5 × 6) ‖ 7) + 10) × 11
= 1 × (2 * 10 + 3) + (((4 × 5 × 6) * 10 + 7) + 10) × 11
= 1 × (2 * 10 + 3) + ((170 * 10 + 7) + 10) × 11
= 1 × (20 + 3) + ((1700 + 7) + 10) × 11
= 1 × (20 + 3) + (1707 + 10) × 11
= 1 × 23 + 1717 × 11
= 23 + 21107
= 21132
Шестнадцатеричная:
2ACE
= 1 × (2‖3) + (((4 × 5 × 6) ‖ 7) + 10) × 11
= 1 × (2 * 10 + 3) + (((4 × 5 × 6) * 10 + 7) + 8) × 9
= 1 × (2 * 10 + 3) + ((78 * 10 + 7) + 8) × 9
= 1 × (20 + 3) + ((780 + 7) + 8) × 9
= 1 × (20 + 3) + (787 + 8) × 9
= 1 × 23 + 78F × 9
= 23 + 4407
= 442A
Но ведь мы выше описали представление числа, которое легко переключается между системами счисления, и без проблем получали одно и тоже результат в разных системах счислениях… Получается проблема в том, мы не применяем операцию перевода системы счисления к операнду, что «обычно» является весьма странным… Но т.к. операция конкатенации напрямую зависит от системы счисления, то получается и к ней нужно приметь перевод.
В целом можно тут развести «хитрые формулы» которые будет переводить систему «на ленту», но для просты, сделаем перевод в другую систему счисления не первой операцией. Т.е. у нас получается так.
Восьмеричная:
10958 — запись в десятичной системе
= 1 × (2‖3) + (((4 × 5 × 6) ‖ 7) + 8) × 9 — запись в десятичной системе
= 1 × (2 * 10 + 3) + (((4 × 5 × 6) * 10 + 7) + 8) × 9 — запись в десятичной системе
= 1 × (2 * 12 + 3) + (((4 × 5 × 6) * 12 + 7) + 10) × 11 — здесь и далее уже восьмеричная система счисления
= 1 × (2 * 12 + 3) + ((170 * 12 + 7) + 10) × 11
= 1 × (24 + 3) + ((2260 + 7) + 10) × 11
= 1 × (24 + 3) + (2267 + 10) × 11
= 1 × 27 + 2277 × 11
= 27 + 25267
25316 – что соответствует 10958
Шестнадцатеричная:
10958 — запись в десятичной системе
= 1 × (2‖3) + (((4 × 5 × 6) ‖ 7) + 8) × 9 — запись в десятичной системе
= 1 × (2 * 10 + 3) + (((4 × 5 × 6) * 10 + 7) + 8) × 9 — запись в десятичной системе
= 1 × (2 * A + 3) + (((4 × 5 × 6) * A + 7) + 8) × 9 — здесь и далее уже шестнадцатеричная система счисления
= 1 × (2 * A + 3) + ((78 * A + 7) + 8) × 9
= 1 × (14 + 3) + ((4B0 + 7) + 8) × 9
= 1 × (14 + 3) + (4B7 + 8) × 9
= 1 × 17 + 4BF × 9
= 1 × 17 + 4BF × 9
= 17 + 2AB7
= 2ACE – что соответствует 10958
Ура. Собственно, получилось)
Получается мы не замечаем целой математической операции который мы пользуемся каждый день. Более того на ней легко выполняются все необходимые правила проверок для операций и это круто. А теперь, я слушаю в чем я не прав? :)
П.с.
Почему я говорю о этой задаче как о «не решенной», хотя кажется, что решение на поверхности.
Задача появилась относительно недавно, но и не слишком распространена. Сама идея конкатенации — не принадлежит мне, оно в сети в свободном доступе, но вот почему-то никто не приводит математического обоснования почему «конкатенация решает».
Оригинальное видео с которого я стал копать тему:
Перевод:
А вот собственно документ с таблицей.
П.п.с.
Taneja вообще интерсный мужик. Вот еще одна большая его статья о числах. В ней он представляет любое число от 0 до 1000 с помощью комбинаций операций над одним числом из множества от 1 до 9:
arxiv.org/pdf/1502.03501.pdf
Был один пробел, а именно число 10958, который немного всколыхнул научное сообщество, и самое главное до сих пор не заполнен. Вот про него мы и поговорим.

Введение
Для начала об самой статье Crazy Sequential Representation… В ней основная часть отведена таблице на 160 листов на которых любое число (от 0 до 11 111) приставлено операциями над двумя последовательностями чисел. Последовательности такие:
* 1, 2, 3, 4, 5, 6, 7, 8, 9
* 9, 8, 7, 6, 5, 4, 3, 2, 1
Например, 2021 представить можно так
* 2021 = 12×(3×4 + 5 + 6)×7 + 89
* 2021 = (9×8 + 7 + 6)×5×4 + 321
А 307 так:
* 307 = 123 + 45 + 67 + 8×9
* 307 = 9×8 + 7×6×5 + 4×3×2 + 1
Важно понимать, что последовательности 1, 2…8, 9 и 9, 8…2, 1 не должны нарушаться при визуальной записи. Более того, набор допустимых операций – это самый базовый «школьный» набор:
* plus (плюс);
* minus (минус);
* product (умножение);
* potentiation (возведение в степень);
* division (деление);
* brackets (скобки)
«Сложные» операции такие как — факториал, квадратный корень и т.д. недопустимы…
Самое удивительное, что все числа, до 11 111, мы можем получить благодаря этим базовым операциям… Ну или почти все… Одно число раскололо математическое сообщество на два лагеря. Это число — 10958. В статье Танежа написано так:
* 10958 = still not available (все еще недоступно)
* 10958= (9 + 8 × 7 × 65 + 4) × 3 − 2 + 1
Т.е. математики сначала загнали себе в рамки, а потом раскололись из-за рамок на два лагеря. Первые сказали — что такая последовательность базовых операций должна существовать, но еще не найдена. Вторые – нашли решение, но схитрили и расширили понятие «базовые операции».
О чем спор
Что бы понять «о чем спор» для начала вернемся к числу 2021 из таблицы. Сейчас это число вычисляется так:
* 2021 = 12×(3×4 + 5 + 6)×7 + 89
Как видно, здесь есть два «странных» числа – это 12 и 89, которые выбиваются из начальных условий. Ибо, из «условий задачи», начальные числа должны быть из следующего множества: 1, 2, 3, 4, 5, 6, 7, 8, 9, а тут появляются 12 и 89… Что не совсем честно… И отсюда и появляется идея у одной из групп математиков. Они ввели новую операцию – «конкатенацию» и сказали, что она «базовая»… Проблема в том, что для операции «конкатенации» даже общепринятого символа нет, а тут её решили причислить к базовым…
И раз никто не знает, как её толком обозначить, а мне статью писать нужно, в дальнейшем, операцию «конкатенации» будем обозначать символом ‖ (т.к. именно это обозначение я встречал чаще всего).
Давайте вспомним свойства конкатенации.
1) Операция конкатенации ассоциативна.
То есть, если нужно выполнить конкатенацию трёх слов, то от расстановки скобок результат не изменится: ( wiki ‖ media ) ‖ pedia = wikimediapedia, и в то же время wiki ‖ ( media ‖ pedia ) = wikimediapedia.
2) Операция конкатенации некоммутативна.
В самом деле, wiki ‖ media = wikimedia, но media ‖ wiki = mediawiki ≠ wikimedia. От перестановки операндов меняется результат операции, что и означает её некоммутативность.
3) Пустое слово — ε, — является нейтральным элементом (единицей) операции конкатенации.
То есть, если ε— пустое слово, то для любого слова α выполнено равенство: ε ‖ a = a ‖ ε = a
4) Длина (количество букв) конкатенации слов равна сумме длин операндов:
|α ‖ β| = |α| + |β|.
Эти свойства вполне себе известны и описаны на википедии.
Добавим еще описание приоритетности:
5) (плюс, минус) < (умножение, деление) < (возведение в степень) < (конкатенация)
И так. Вернемся к таблице Танежа, а именно числу 2021.
Напомню, сейчас это число записано так: 2021 = 12×(3×4 + 5 + 6)×7 + 89.
Так вот, с вводом «новой» операции, это число будет записано так:
* 2021 = (1 ‖ 2) × (3 × 4 + 5 + 6) × 7 + (8 ‖ 9).
В целом поменялся только формат записи. Всё остальное работает, как и раньше. Но фокус в том, что в таком случае, математики нашли решение для числа 10958.
* 10958 = 1 × (2‖3) + (((4 × 5 × 6) ‖ 7) + 8) × 9
Пояснение:
1 × (2‖3) + (((4 × 5 × 6) ‖ 7) + 8) × 9
= 1 × 23 + ((120 ‖ 7) + 8) × 9
= 1 × 23 + (1207 + 8) × 9
= 1 × 23 + 1215 × 9
= 23 + 10935
= 10958
И вот на этом обычно все видосики и статьи заканчиваются, показываю вот такой вот математический фокус и оставляя всех размышлять на чьей стороне зритель… А, я продолжу. Ибо фокус открывается весьма интересный пласт операций.
А теперь уже мои размышления
Начнем с того — почему эта операция вообще не нравится первой группе ученых.
Операция «конкатенация» вообще не считается арифметической операцией… Это операция склеивания объектов линейной структуры, обычно строк, что собственно и это собственно отталкивает «первую» часть математиков. Они говорят — мол, нужно делать математические операции, а не «хаки»… Поэтому я попробую перевести операцию конкатенации в алгебраическую плоскость и более того постараюсь показать, что операция вполне базовая, а потом готов выслушать ваше мнение, о том где я не прав.
Алгебраическое представление конкатенации
В действительности все натуральные числа можно представить через операцию конкатенации: 1‖0‖9‖5‖8. И дабы показать, что эту операцию можно отнести к базовым немного попрыгаем по системам счисления.
Возьмем число 10958 в разных представлениях:
Двоичная: 10 1010 1100 1110 = 1‖0‖1‖0‖1‖0‖1‖1‖0‖0‖1‖1‖1‖0
Восьмеричная: 25316 = 2‖5‖3‖1‖6
Шестнадцатеричная 2ACE = 2‖A‖C‖E = 2‖10‖12‖14
Ого, в шестнадцатеричной система стало еще интересней, оказывается через операцию конкатенации мы можем выражать числа используя не только «хак» с буквами A, B, C, D, E, F, но и через стандартные арабские числа от 0 до 16… Хотя стоп… Сверху мы описали операцию конкатенации немного не так. Т.е. для случая 2‖10‖12‖14 мы получаем совсем другое число. Получается нам нужно поменять определение операции «конкатенации», которую мы применяем к числам, так, давайте сделаем это. Но для начала вспомним представления других операций.
Умножение можно представить как:

Возведение в степень:

Школьный курс вспомнили, теперь вспомни, что еще в школьном курсе было умножение на 10. Которое позволяло «подставлять числа сзади». Ну т.е.:
* 1‖0‖9‖5‖8 = (((1 * 10 + 0) * 10 + 9) * 10 + 5) * 10 + 8.
Итого мы разложили операцию «конкатенации» так: a ‖ b = (a * 10) + b; Но 10 — это хитрое число… Это число следующие за максимальным из группы в системе счисления, ну т.е. это просто основание системы счисления т.е. общий вид такой:
a ‖ b = (a * m) + b, где m – основание системы счисления представленное в обозначении самой системы.
Но такое определение мне не очень нравится, ибо m больше чем возможные числа внутри системы. Давайте сделаем чуть хитрее.
 ,
, где — это целое число означающее 1 в системе счисления, а — основание системы счисления. Т.е. мы по факту складываем палочки. Вот теперь получилось красиво с точки зрения определения, но
a ‖ b = (a * 10) + b – легче для восприятия.
Давайте, на всякий случай, проверим, что действительно это работает и пересчитаем описанные выше операции на 10958.
Двоичная: 10 1010 1100 1110 = 1‖0‖1‖0‖1‖0‖1‖1‖0‖0‖1‖1‖1‖0 = ((((((((((((1 * 10 + 0) * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 1) * 10 + 0) * 10 + 0) * 10 + 1) * 10 + 1) * 10 + 1) * 10 + 0

Восьмеричная: 25316 = 2‖5‖3‖1‖6 = (((2 * 10 + 5) * 10 + 3) * 10 + 1) * 10 + 6

Шестнадцатеричная 2ACE = 2‖A‖C‖E = ((2 * 10 + A) * 10 + C) * 10 + E

Собственно, в таком определении операции конкатенации, мы перевели её в алгебраическую плоскость. Причем свойства операции, написанные выше, сохраняются.
Получается мы решили загадку числа 10958? Ну… Давайте проверим. Получается, что мы должны изменив систему счисления получить те же данные из таблицы Танежа.
Возьмем к примеру число: 238 (в нем важно, что все числа в решении стоят отдельно), тогда получаем:
Десятичная:
238
= 1 + 2×3 + 4 + 5×6×7 + 8 + 9
= 1 + 6 + 4 + 210 + 8 + 9
= 238
Восьмеричная (т.е. 8 = 10, 9 = 11):
356
= 1 + 2×3 + 4 + 5×6×7 + 10 + 11
= 1 + 6 + 4 + 322 + 10 + 11
= 356
Шестнадцатеричная:
EE
= 1 + 2×3 + 4 + 5×6×7 + 8 + 9
= 1 + 6 + 4 + D2 + 8 + 9
= EE
В итоге мы получаем, что результат сохраняются при переводе чисел в другую систему счисления, что собственно логично и круто. А вот с введением нашей операции «конкатенации» так не получается…
Десятичная:
10958
= 1 × (2‖3) + (((4 × 5 × 6) ‖ 7) + 8) × 9
= 1 × (2 * 10 + 3) + (((4 × 5 × 6) * 10 + 7) + 8) × 9
= 1 × (2 * 10 + 3) + ((120 * 10 + 7) + 8) × 9
= 1 × (20 + 3) + ((1200 + 7) + 8) × 9
= 1 × 23 + (1207 + 8) × 9
= 1 × 23 + 1215 × 9
= 23 + 10935
= 10958
Восьмеричная (т.е. 8 = 10, 9 = 11):
25316
= 1 × (2‖3) + (((4 × 5 × 6) ‖ 7) + 10) × 11
= 1 × (2 * 10 + 3) + (((4 × 5 × 6) * 10 + 7) + 10) × 11
= 1 × (2 * 10 + 3) + ((170 * 10 + 7) + 10) × 11
= 1 × (20 + 3) + ((1700 + 7) + 10) × 11
= 1 × (20 + 3) + (1707 + 10) × 11
= 1 × 23 + 1717 × 11
= 23 + 21107
= 21132
Шестнадцатеричная:
2ACE
= 1 × (2‖3) + (((4 × 5 × 6) ‖ 7) + 10) × 11
= 1 × (2 * 10 + 3) + (((4 × 5 × 6) * 10 + 7) + 8) × 9
= 1 × (2 * 10 + 3) + ((78 * 10 + 7) + 8) × 9
= 1 × (20 + 3) + ((780 + 7) + 8) × 9
= 1 × (20 + 3) + (787 + 8) × 9
= 1 × 23 + 78F × 9
= 23 + 4407
= 442A
Но ведь мы выше описали представление числа, которое легко переключается между системами счисления, и без проблем получали одно и тоже результат в разных системах счислениях… Получается проблема в том, мы не применяем операцию перевода системы счисления к операнду, что «обычно» является весьма странным… Но т.к. операция конкатенации напрямую зависит от системы счисления, то получается и к ней нужно приметь перевод.
В целом можно тут развести «хитрые формулы» которые будет переводить систему «на ленту», но для просты, сделаем перевод в другую систему счисления не первой операцией. Т.е. у нас получается так.
Восьмеричная:
10958 — запись в десятичной системе
= 1 × (2‖3) + (((4 × 5 × 6) ‖ 7) + 8) × 9 — запись в десятичной системе
= 1 × (2 * 10 + 3) + (((4 × 5 × 6) * 10 + 7) + 8) × 9 — запись в десятичной системе
= 1 × (2 * 12 + 3) + (((4 × 5 × 6) * 12 + 7) + 10) × 11 — здесь и далее уже восьмеричная система счисления
= 1 × (2 * 12 + 3) + ((170 * 12 + 7) + 10) × 11
= 1 × (24 + 3) + ((2260 + 7) + 10) × 11
= 1 × (24 + 3) + (2267 + 10) × 11
= 1 × 27 + 2277 × 11
= 27 + 25267
25316 – что соответствует 10958
Шестнадцатеричная:
10958 — запись в десятичной системе
= 1 × (2‖3) + (((4 × 5 × 6) ‖ 7) + 8) × 9 — запись в десятичной системе
= 1 × (2 * 10 + 3) + (((4 × 5 × 6) * 10 + 7) + 8) × 9 — запись в десятичной системе
= 1 × (2 * A + 3) + (((4 × 5 × 6) * A + 7) + 8) × 9 — здесь и далее уже шестнадцатеричная система счисления
= 1 × (2 * A + 3) + ((78 * A + 7) + 8) × 9
= 1 × (14 + 3) + ((4B0 + 7) + 8) × 9
= 1 × (14 + 3) + (4B7 + 8) × 9
= 1 × 17 + 4BF × 9
= 1 × 17 + 4BF × 9
= 17 + 2AB7
= 2ACE – что соответствует 10958
Ура. Собственно, получилось)
Получается мы не замечаем целой математической операции который мы пользуемся каждый день. Более того на ней легко выполняются все необходимые правила проверок для операций и это круто. А теперь, я слушаю в чем я не прав? :)
П.с.
Почему я говорю о этой задаче как о «не решенной», хотя кажется, что решение на поверхности.
Задача появилась относительно недавно, но и не слишком распространена. Сама идея конкатенации — не принадлежит мне, оно в сети в свободном доступе, но вот почему-то никто не приводит математического обоснования почему «конкатенация решает».
Оригинальное видео с которого я стал копать тему:
Перевод:
А вот собственно документ с таблицей.
П.п.с.
Taneja вообще интерсный мужик. Вот еще одна большая его статья о числах. В ней он представляет любое число от 0 до 1000 с помощью комбинаций операций над одним числом из множества от 1 до 9:
arxiv.org/pdf/1502.03501.pdf





