Как устроено множество Мандельброта. Центральная кардиоида

Хорошо известно, что центральная часть множества Мандельброта представляет из себя кардиоиду. Не просто похожа, а именно ей и является. Сегодня мы пытаемся понять, почему именно кардиоида и что из этого следует.

Данная статья продолжает серию об устройстве множества Мандельброта. Ранее мы изучали свойства возведения в квадрат в комплексной плоскости. Сегодня продвигаемся чуть дальше.


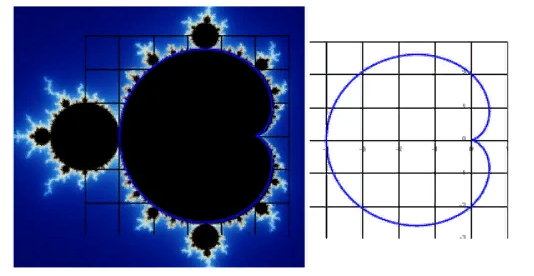
Фиг.1 Аналитически построенная кардиоида, наложенная на множество Мандельброта. Отсюда.


Интуитивно понятно, что точки кардиоиды порождают в некотором смысле предельные траектории. По аналогии, когда ранее мы разбирали как устроено комплексное возведение в квадрат, такие предельные точки были на единичной окружности. Всё что внутри окружности, быстро схлопывается в ноль. Всё что вне окружности, улетает в бесконечность. Интересны лишь эти предельные точки.


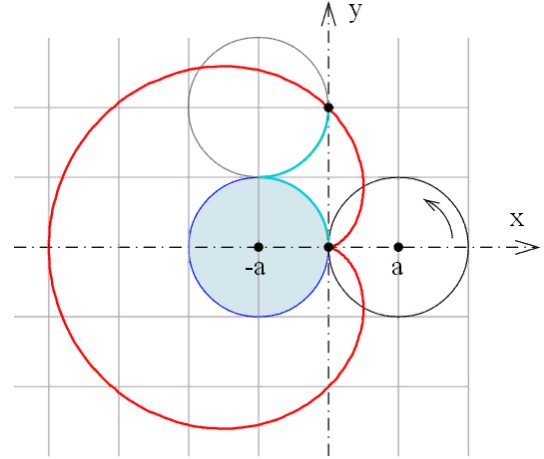
Фиг.2 построение кардиоиды. Отсюда.

Уравнение в прямоугольных координатах:
$\$inline\$\backslash \backslash x=2\; a\; \backslash cos(\phi )+a\backslash cos(2\phi )\backslash \backslash \; y=2\; a\; \backslash sin(\phi )+a\backslash sin(2\phi )\$inline\$$
в нашем случае a=¼

Как и раньше, наш излюбленный тактический приём — «хватит думать, давайте просто посмотрим что там». Поэтому возьмём несколько точек с кардиоиды и посмотрим, что их объединяет.
Начнём с (0.25, i*0.5) просто потому что координаты круглые.


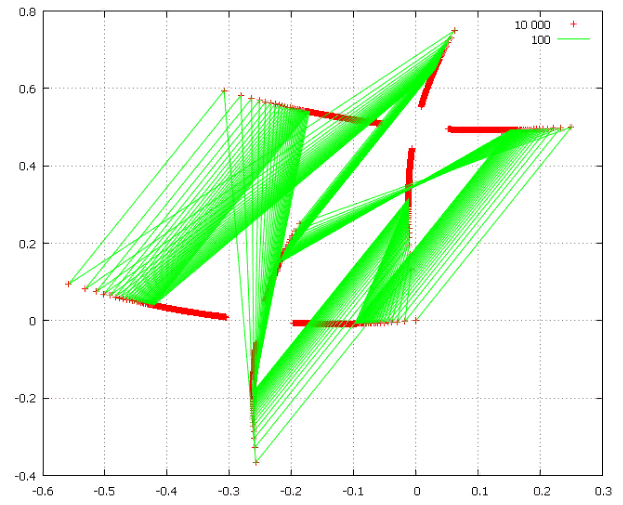
Фиг.3 Последовательность, соответствующая константе (0.25, i*0.5).

Константа соответствует углу кардиоиды φ=π/2.

Показаны первые 100 (линиями, для наглядности) и первые 10 000 (точками) переходов. Каждый переход показан в виде двух отрезков/точек — возведение в квадрат и сдвиг на константу.

Похоже, цикл стягивается в точку (0, i*0.5). Легко заметить, что (0, i*0.5) при возведении в квадрат превращается (-0.25, i*0), добавляя к которой константу снова получаем (0, i*0.5). А еще точка (0, i*0.5) лежит на окружности с радиусом 0.5 при угле π/2. И параметр кардиоиды был φ=π/2. Совпадение? Возможно.

Проверяем гипотезу, что константы с кардиоиды стягиваются в точки на окружности с радиусом 0.5. По этой окружности при построении кардиоиды перемещается центр движущейся окружности.

1. угол φ=0, константа на кардиоиде (0.25, i*0). Стягивается к точке (0.5, i*0).
   $$
   так и есть
2. угол $$, константа на кардиоиде (-0.75, i*0). Стягивается к точке (-0.5, i*0).
   Смотрим картинку.
   
   
   
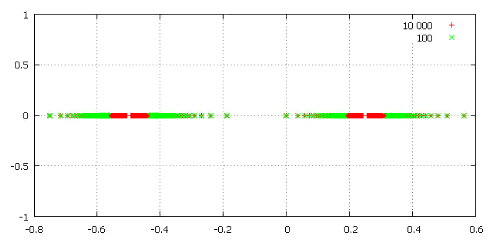
   Фиг.4 Последовательность, соответствующая константе (-0.75, i*0).
   
   Здесь для наглядности только точки.
   $$
   
3. Возьмём навскидку, $$
   Смотрим картинку.
   
   
   
   
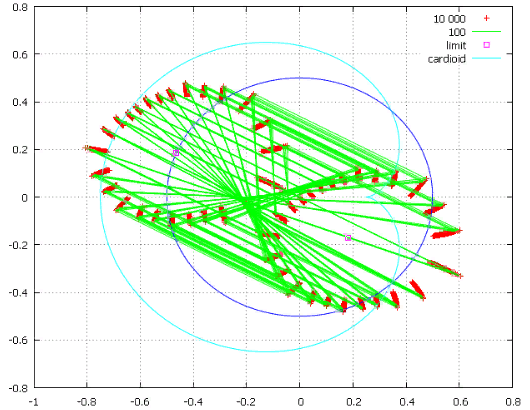
   Фиг.5 Последовательность, соответствующая $$.
   
   Первые 100 переходов показаны линиями, остальные обозначены только точками.
   Да, траектория стягивается к точке на окружности с радиусом ½ и углом 0.88π. Сходится, правда, не очень резво. Проверяем:
   
   (-0.46488824294, i* 0.18406227634) => (0.18224215685, i*-0.17113677648)
   (0.18224215685, i*-0.17113677648) => (-0.46488824294, i* 0.18406227634)
   Всё верно, эти предельные точки обозначены выше квадратиками как 'limit’.
   

Наверняка это как-то можно получить в аналитической форме. Попробуем.

1. Точка на предельной окружности с радиусом ½.
   x = ½ cos (φ)
   y = ½ sin (φ)
   на самом деле это комплексное число (½ cos (φ), ½ i sin (φ))
   
2. Возводим комплексное число в квадрат, получаем
   (¼ cos (2φ), ¼ i sin (2φ))
3. Константа (пусть С) для этого угла находится на кардиоиде, по формуле:
   Re(С) = ½ cos (φ) — ¼ cos (2φ)
   Im(С) = ½ sin (φ) — ¼ sin (2φ)
4. Складываем и получаем
   (½ cos (φ), ½ i sin (φ))
5. Что и требовалось доказать

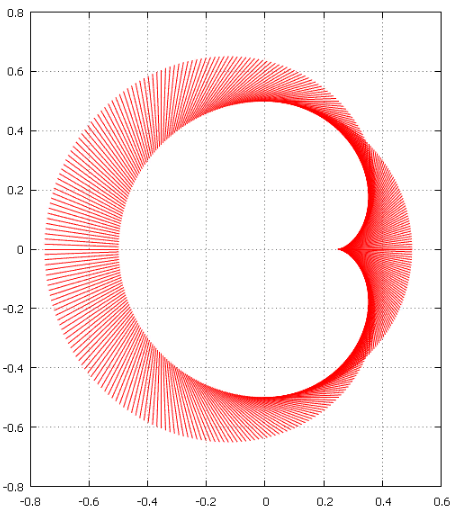
Фиг.6 Соответствие кардиоиды и предельной окружности. Шаг — 1 градус.
В двух точках они пересекаются.

Хозяйке на заметку, последовательность $\$inline\$¼\; +\; (¼\; +\; (¼\; +\; (¼\; +\; (¼\; +\; \dots \; )^2)^2)^2)^2\$inline\$$ сходится к ½ что на первый взгляд не так уж и тривиально.

Обобщаем

Последовательности, стартующие с кардиоиды, сходятся к точкам на окружности. А что с другими точками, куда сходятся они, нет ли более общей закономерности?

Попробуем.

1. Исходная точка
   $$
2. Сходится к искомой точке
   $$
3. Возводим комплексное число в квадрат, получаем
   $$
4. Складываем с константой и получаем
   $\$inline\$r^2cos\; (2\phi )\; +\; x\_0\; =\; r\backslash cos\; (\phi )\backslash \backslash \; r^2sin\; (2\phi )\; +\; y\_0\; =\; r\backslash sin\; (\phi )\backslash \backslash \$inline\$$
   $\$inline\$r^2(2\; \backslash cos^2\; (\phi )\; -\; 1)\; -\; r\backslash cos\; (\phi )\; +\; x\_0\; =\; 0\backslash \backslash \; r\backslash sin\; (\phi )\; (2\; r\; \backslash cos\; (\phi )\; -\; 1)\; +\; y\_0\; =\; 0\backslash \backslash \$inline\$$
   $\$inline\$r\backslash cos\; (\phi )\; (2\; r\backslash cos\; (\phi )\; -\; 1)\; -\; r^2+\; x\_0\; =\; 0\backslash \backslash \; r\backslash sin\; (\phi )\; (2\; r\backslash cos\; (\phi )\; -\; 1)\; +\; y\_0=\; 0\backslash \backslash \$inline\$$
   $$
   
5. Или, что то же самое
   $$
   это обратная задача — получение констант из финальных точек
6. Прямая задача, если нужны x, y из $$
   $$
   
   $$
   …
   

Кстати, в качестве проверки, если x и y поместить на окружность радиусом 0.5,
$$ должны оказаться на кардиоиде.


Фиг.7 Аналитически полученные константы для предельных точек с разных окружностей.

Здесь показаны результаты решения обратной задачи — по финальным окружностям с центром в начале координат и разными радиусами получены константы С множества Мандельброта.

1. Как и ожидалось, для окружности с радиусом 0.5 константы находятся на кардиоиде.
2. Точка (0.25, 0i) изрядно особая, все три кривые её касаются.
3. Все три случая описываются одной кривой — это улитка Паскаля.
4. Кардиоида — вырожденный случай улитки Паскаля.
5. В силу п.2 в улитке синхронно меняются два параметра — радиус окружностей и смещение на радиус векторе подвижной окружности.

Но позвольте, скажет внимательный читатель, константы для предельной окружности с радиусом 0.6 находятся за пределами множества Мандельброта, как же они могут иметь предельные точки?

Фокус вот в чем. Если бы последовательность с такой константой смогла достичь предельной точки, то упокоилась бы в ней с миром. Но она не может в нее попасть. Если для констант внутри или на кардиоиде предельные точки являются притягивающими, то для остальных — отталкивающими.

Разберем на примере. Сначала простой случай — движение по реальной оси, положительной её части.

Для реальных чисел всё сводится к $$. Это рекуррентное уравнение можно представить следующим образом


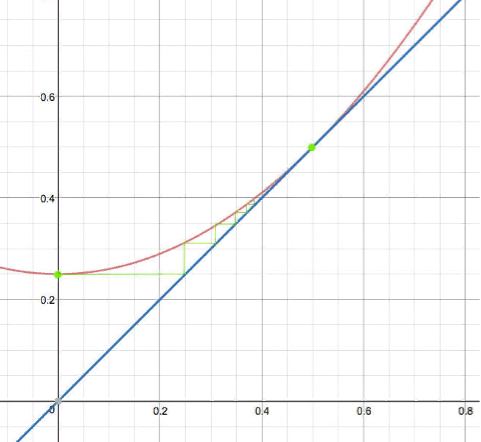
Фиг.8 представление рекуррентной последовательности для С=0.25. Отсюда.

Зеленым показана собственно последовательность, которая “бьётся” между
$$ и $$.
Будь константа чуть больше (0.26), между $$ и $$ осталась бы щель. Последовательность проскользнула бы в эту щель и начала разгоняться.

Если чуть меньше (0.24), $$ и $$ сомкнулись бы с приличным углом и последовательность сошлась бы намного быстрее.

С комплексными константами принципиально всё то же, но не так очевидно. Для наглядности возьмём уже знакомую точку на кардиоиде с $$ и построим траектории с небольшими отклонениями от нее.


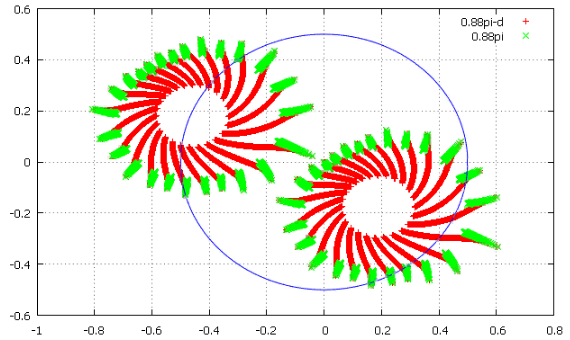
Фиг.9 отклонение на 0.0001 вправо.

Здесь уже знакомые нам первые 10 000 переходов с кардиоиды (угол 0.88π) под меткой “0.88pi” и 10 000 точек траектории, которая начинается на 0.0001 больше по X (т.е. внутрь кардиоиды) (“0.88pi-d”). Разница существенная, сходится гораздо быстрее. Возьмём для наглядности большее возмущение, 0.001.


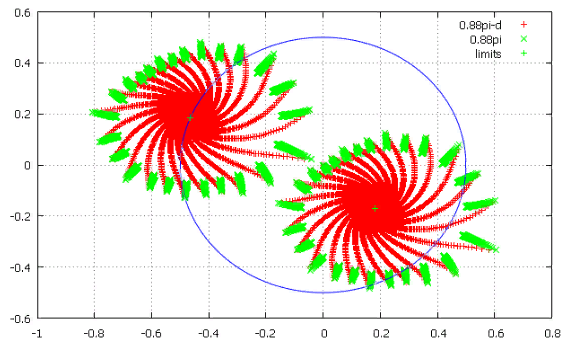
Фиг.10 отклонение на 0.001 вправо.


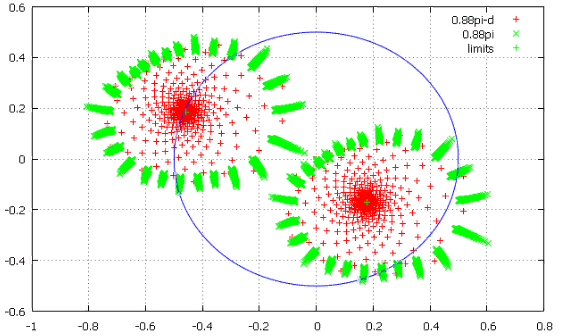
Фиг.11 отклонение на 0.01 вправо. Отчетливо видно что предельная точка не лежит на предельной окружности.


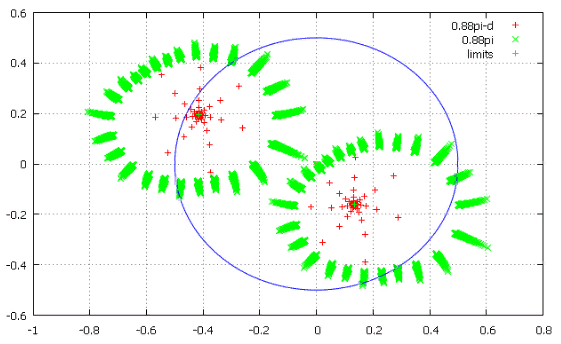
Фиг.12 отклонение на 0.1 вправо.

И наконец.


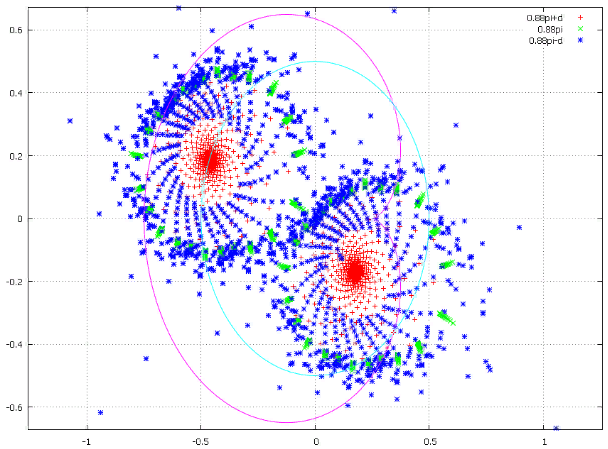
Фиг.13 Старт с точек внутри, на и вне кардиоиды.

При сдвиге наружу от кардиоиды сначала последовательность стремится к предельной точке, потом протискивается в “щель”, после чего начинает стремительно разгоняться наружу.

Вообще, снаружи от кардиоиды следует быть очень осторожным, легко наступить во фрактальную «бахрому», с которой станем разбираться позже.

И напоследок.


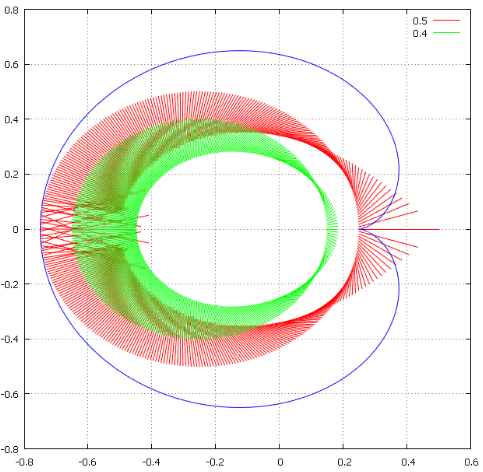
Фиг.14 вычисленные итерационным путём финишные точки внутри кардиоиды. Легко проверить по формулам.

Численный эксперимент. Здесь мы стартуем с окружностей со смещенным центром (-0.25, i*0) и радиусами 0.4 и 0.5. Шаг сканирования — 1 градус. Показаны начальная и конечная точки последовательности, ограниченной 1000 итераций. Хаос, возникший при приближении окружности с радиусом 0.5 к углу π вызван тем, что в этой окрестности наша стартовая окружность смыкается с кардиоидой и сходимость последовательности замедляется. 1000 итераций просто не хватило, чтобы прийти к предельной точке.

Вот так, с помощью Википедии и математики школьного уровня, мы более-менее выяснили что происходит внутри центральной кардиоиды.

В следующий раз займёмся “хвостом” множества Мандельброта — отрицательной частью реальной оси константы и её окрестностями.